The 19th Zhejiang University Programming Contest Sponsored by TuSimple (Mirror) B"Even Number Theory"（找规律？？？）

传送门

题意：

　　给出了三个新定义：

1. E-prime : ∀ num ∈ E，不存在两个偶数a,b，使得 num=a*b;（简言之，num的一对因子不能全为偶数）
2. E-prime factorization : 定义集合P由 E-prime 元素组成，定义 e = p₁*p₂*.....*p_n；（p₁,p₂,....,p_n ∈ P , |P| = n）
3. E-factorial : 定义 e!! = 2*4*6*8*.........*e；（简言之，偶数e及其之前的偶数连乘积）

　　输出一个数 e ，求满足条件2的集合P，并且集合P需满足：p₁*p₂*.....*p_n = e!! , |P| = n；

　　求 n 的最大值；

 题解：

　　定义集合 P_i 为偶数 i 的满足条件（2）的最大的集合；

　　例如P₈ = {2,2,2}，| P₈ | = 3；

　　根据贪心的思想，要想使集合 P_e!! 中的元素个数最多，那么，e!! 一定要优先分解出最多的2（最小的e-prime）;

　　定义 odd 表示奇数，那么 odd*2 为 e-prime，因为 odd 因式分解肯定没有偶数因子，odd*2 只能分解出一个偶数因子2，符合条件（1）；

　　因此，对于所有的奇数 odd，可以通过让 odd*2 将 odd 转化为 e-prime，那么，我们的关注点就变成了 e!! 最多能分解出多少个2；

　　对于 e 之前的所有偶数，假设 ≤ e 的最大的2的幂为 2^x+1，那么对于 e 之前的所有2的幂 2¹,2²,2³,....,2^x+1 其可分解出 1+2+3+......+x+1 个2；

　　那 e 之前的所有非2的幂的偶数 even ，该如何快速求出他们的乘积最多能分解出多少个2呢？

　　首先，求解一下 2^x+1 及其之前的偶数乘积最多可以分解出多少个2；

　　首先考虑这一点，任何一个偶数 even 都可分解成 odd*2ⁱ 模式， 那么 |P_even | = i；

　　那么，我们反过来考虑，对于任意奇数 odd 都可通过 odd*2ⁱ 求出 | P_odd*2ⁱ | = i;

　　

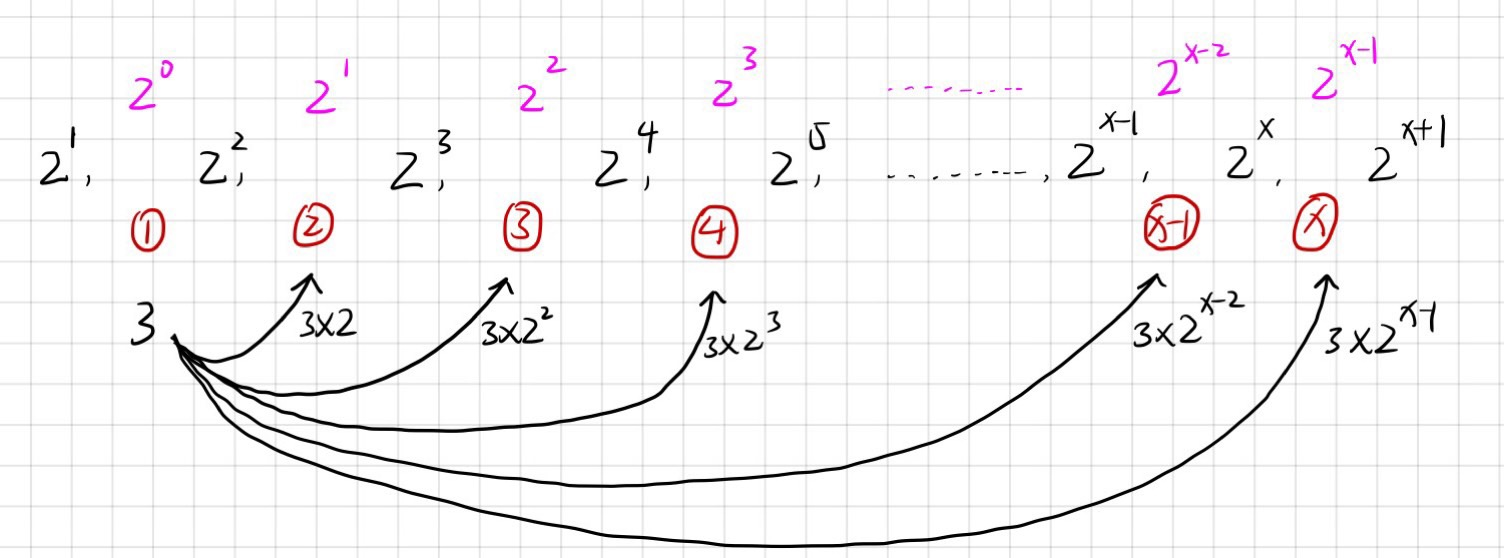
　　　　　　（每两个相邻的2的幂间的偶数块用红色编号① ② ③ ④ ...........表示）

　　　　　　（紫色数字代表相邻的2的幂间的奇数的个数）

　　对于偶数块①：只有一个奇数 3；

　　3*2¹ 来到偶数块②；

　　3*2² 来到偶数块③；

　　3*2³ 来到偶数块④；

　　........

　　3*2^x-1来到偶数块(x)；

　　（注意偶数块的编号和2的幂的关系）

　　可知，通过3*2ⁱ 可求出P_3*2¹ , P_3*2² , .........., P_3*2^x-1，其集合元素个数总和为 1+2+3+..........+(x-1);

　　那么，对于偶数块 2 中的某一奇数 odd 呢？

　　根据对3的分析，可知，偶数块②可以构成的 ≤ 2^x+1 的最大的偶数为 odd*2^x-2 ，那么，通过 odd 求出的集合P_odd*2ⁱ 的元素个数总和为 1+2+3+.......+(x-2)

　　因为偶数块②有2¹个奇数，所以这些奇数可以求出的集合P的元素个数总和为 2*(1+2+3+........+(x-2) ）;

　　偶数块③有2²个奇数，其中任意一个 odd 可构成的 ≤ 2^x+1 的最大的偶数为 odd*2^x-3 ，这些奇数可以求出的集合P的元素个数总和为 2²*(1+2+......+(x-3) );

　　..............

　　偶数块(x-1)有2^x-2个奇数，其可求出的集合P的元素个数总和为2^x-2;

　　综上，2x+1 及其之前的偶数乘积最多可以分解出的2的个数为：

　　

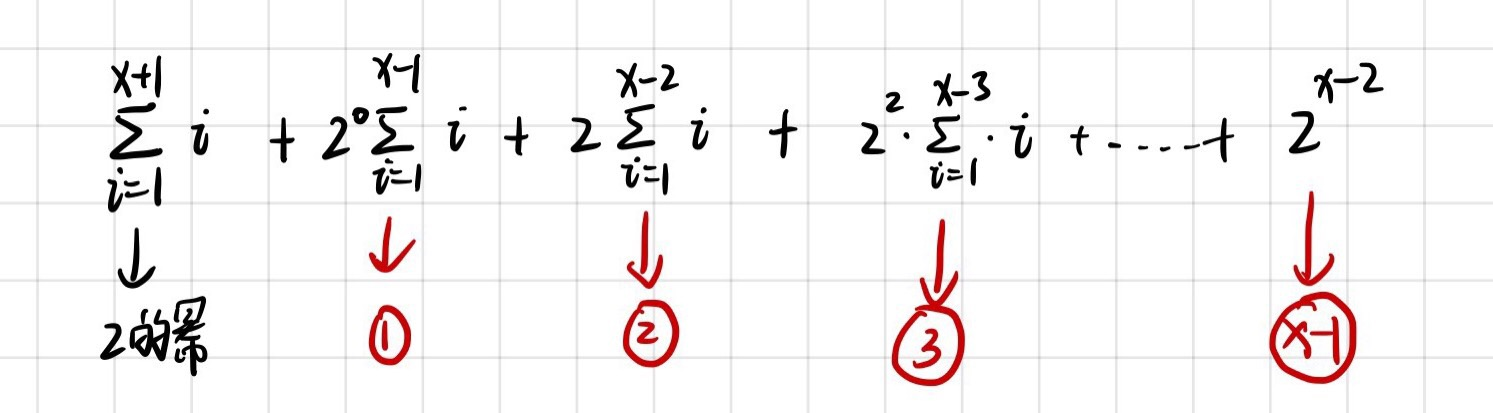
　　这几项加和的值等于 2^x+1-1；

　　（并不是通过公式化简成这个最简式，而是通过打表找到的，公式化简的话，只能依靠那些大佬了QWQ）

　　打表推公式代码：（明天张贴）

 #include<iostream>
 #include<cstdio>
 using namespace std;

 int Sum(int pow,int up)
 {
     int sum=;
     for(int i=;i <= up;++i)
         sum += i;
     return sum*pow;
 }
 int main()
 {
     int x;
     while(~scanf("%d",&x))
     {
         int sum=Sum(,x);
         int base=;
         for(int i=;i <= x-;++i)
         {
             sum += Sum(base,x--i);
             base *= ;
         }
         printf("sum=%d,%d\n",sum,<<x);
     }
 }

　　那么，如果 e 为2的幂，直接输出 e-1；

　　如果不是，先求出 ≤ e 的最大的2的幂 2^x+1 ，记录当前答案 ans = 2^x+1-1;

　　那[2^x+1 , e]之间的解该如何求出呢？

　　还是考虑 odd*2ⁱ 的模式；

　　令 odd1 ∈ [ 2^x+1 / 2 , e / 2]，∀odd1 * 2 ∈ [ 2^x+1 , e ]，且为 e-prime，ans += tot1*1;(tot为奇数个数)

　　令 odd2 ∈ [ 2^x+1 / 4 , e / 4]，∀odd2 * 4 ∈ [ 2^x+1 , e ]，且为 e-prime，ans += tot2*2;

　　.............

　　令 oddk ∈ [ 2^x+1 / 2^k , e / 2^k]，∀oddk * 2^x ∈ [ 2^x+1 , e ]，且为 e-prime，ans += totk*k;

　　结束的条件是  2^x+1 / 2^k = e / 2^k；

AC代码：（C++版大数伪码）（明天张贴）

 #include<iostream>
 #include<cstdio>
 using namespace std;
 #define BigInteger long long

 BigInteger e;
 BigInteger base;

 BigInteger F()
 {
     BigInteger curBase=;
     BigInteger ans=;
     BigInteger l=base/curBase;
     BigInteger r=e/curBase;
     for(int i=;i < ;++i)
     {
 //        cout<<l<<' '<<r<<endl;
         if(l >= r)
             break;
         BigInteger tmp=(r-l)/;
         if(r&)
             tmp++;
         ans=ans+tmp*i;
         l=l/;
         r=r/;
     }
     return ans;
 }
 void Solve()
 {
     base=;
     while(base* <= e)
         base *= ;
     BigInteger ans=base-;

     if(base != e)
         ans=ans+F();

     cout<<ans<<endl;
 }
 int main()
 {
     int test;
     while(cin>>test)
     {
         while(test--)
         {
             cin>>e;
             Solve();
         }
     }
     return ;
 }

C++版 BigInteger（逃）

AC代码：（Java BigInteger类）（明天张贴）

 import java.math.BigInteger;
 import java.util.Scanner;

 public class Main {

     static Scanner cin = new Scanner(System.in);
     static BigInteger e,base;
     static BigInteger zero=BigInteger.valueOf(0);
     static BigInteger one=BigInteger.valueOf(1);
     static BigInteger two=BigInteger.valueOf(2);
     public static void main(String[] args) {

         int test;
         while(cin.hasNext()) {
             test=cin.nextInt();
             for(int i=1;i <= test;++i) {

                 e=cin.nextBigInteger();
                 Solve();
             }
         }
     }
     private static void Solve() {

         base=one;
         while(base.multiply(two).compareTo(e) <= 0)
             base=base.multiply(two);
 //        System.out.println(base);
         BigInteger ans=base.subtract(one);

         if(!base.equals(e))
             ans=ans.add(F());
         System.out.println(ans);
     }
     private static BigInteger F() {

         BigInteger curBase=two;
         BigInteger ans=zero;
         BigInteger l=base.divide(curBase);
         BigInteger r=e.divide(curBase);
         for(int i=1;i < 4000;++i) {

             if(l.compareTo(r) >= 0)
                 break;
             BigInteger tmp=(r.subtract(l)).divide(two);
             if(r.mod(two).intValue() != 0)
                 tmp=tmp.add(one);
             ans=ans.add(tmp.multiply(BigInteger.valueOf(i)));

             l=l.divide(two);
             r=r.divide(two);
         }
         return ans;
     }
 }

今晚比较嗨，比较尽兴；

陪俺家宝宝乘轻轨去市里疯了一圈，返程的路上还做过了一站；

哈哈哈，要一直陪着宝宝啊*_*