[Codeforces Round #433][Codeforces 853C/854E. Boredom]

题目链接：853C - Boredom/854E - Boredom

题目大意：在\(n\times n\)的方格中，每一行，每一列都恰有一个被标记的方格，称一个矩形为漂亮的当且仅当这个矩形有两个角是被标记的方格（这样的矩形有\(\frac{n(n-1)}{2}\)个）。给出\(q\)组询问，询问为一个二维区间，问有多少个漂亮的矩形与之相交。

题解：考虑每一个询问，将题中的方格分为如图所示9个区间

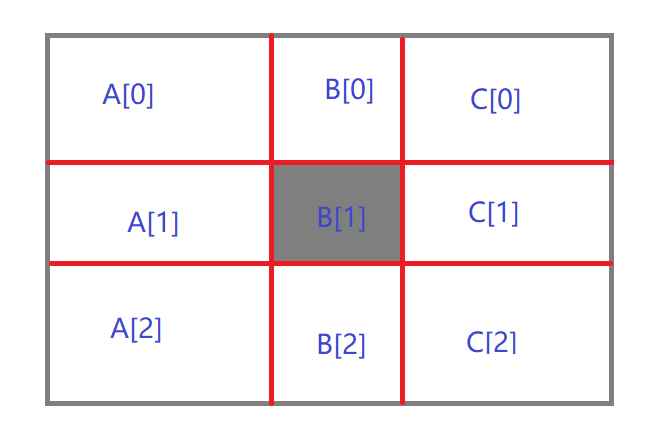
　　每个区间上的数字表示该区间内包含的被标记的点的个数，其中B[1]是询问的区域，为闭区间

　　将这些区间标记出来后，经过分类讨论即可得出答案

　　询问区间内点的个数可以通过二维树状数组来解决，但在这题里空间是肯定不够的，所以需要对询问离散化处理，然后离线做

#include<bits/stdc++.h>
using namespace std;
#define N 200001
struct rua{
    int l,u,r,d,id,a[],b[],c[];
    void read(){scanf("%d%d%d%d",&l,&u,&r,&d);}
    long long get()
      {
      long long res=;
      a[]-=a[],a[]-=a[];
      b[]-=b[],b[]-=b[];
      c[]-=c[],c[]-=c[];
      for(int i=;i<;i++)c[i]-=b[i],b[i]-=a[i];
      res+=1ll*a[]*(b[]+c[]+b[]+c[]);
      res+=1ll*a[]*(b[]+c[]+b[]+c[]+b[]+c[]);
      res+=1ll*a[]*(b[]+c[]+b[]+c[]);
      res+=1ll*c[]*(b[]+b[]);
      res+=1ll*c[]*(b[]+b[]+b[]);
      res+=1ll*c[]*(b[]+b[]);
      res+=1ll*b[]*(b[]+b[]);
      res+=1ll*b[]*b[];
      res+=1ll*b[]*(b[]-)/2ll;
      return res;
      }
}q[N];
int n,m,p[N],t[N];
long long ans[N];
queue<int>Q;
int lowbit(int x){return x&(-x);}
bool cmp1(rua x,rua y){return x.l<y.l;}
bool cmp2(rua x,rua y){return x.r<y.r;}
void change(int x){while(x<N)t[x]++,x+=lowbit(x);}
int ask(int x){int res=;while(x>)res+=t[x],x-=lowbit(x);return res;}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)
      scanf("%d",&p[i]);
    for(int i=;i<=m;i++)
      q[i].read(),q[i].id=i;
    sort(q+,q+m+,cmp1);
    int cur=;
    for(int i=;i<=m;i++)
      {
      while(cur<q[i].l)change(p[cur]),cur++;
      q[i].a[]=ask(q[i].u-),
      q[i].a[]=ask(q[i].d),
      q[i].a[]=ask(N-);
      }
    cur=;
    sort(q+,q+m+,cmp2);
    memset(t,,sizeof(t));
    for(int i=;i<=m;i++)
      {
      while(cur<q[i].r)cur++,change(p[cur]);
      q[i].b[]=ask(q[i].u-),
      q[i].b[]=ask(q[i].d),
      q[i].b[]=ask(N-);
      }
    for(int i=cur+;i<=n;i++)change(p[i]);
    for(int i=;i<=m;i++)
      q[i].c[]=ask(q[i].u-),
      q[i].c[]=ask(q[i].d),
      q[i].c[]=ask(N-);
    for(int i=;i<=m;i++)
      {
      int x=q[i].id;
      ans[x]+=q[i].get();
      }
    //for(int i=1;i<=m;i++)
      //for(int j=0;j<3;j++)
        //printf("%d %d %d\n",q[i].a[j],q[i].b[j],q[i].c[j]);
    for(int i=;i<=m;i++)
      printf("%I64d\n",ans[i]);
}

在我的代码中，是先考虑了漂亮矩形的左边界在\(l\)左边的情况，然后加上整体在\(l\)的右边且右边界在\(r\)右边的漂亮矩形数，最后加上整体在\([l,r]\)中的矩形个数