GNOME图形界面的基本操作

　　成功登录进入CentOS系统之后，我们首先看到的桌面就是GNOME图形界面，下面来看一下相关的基本操作。

个性化设置

1，设置屏幕分辨率

进入菜单

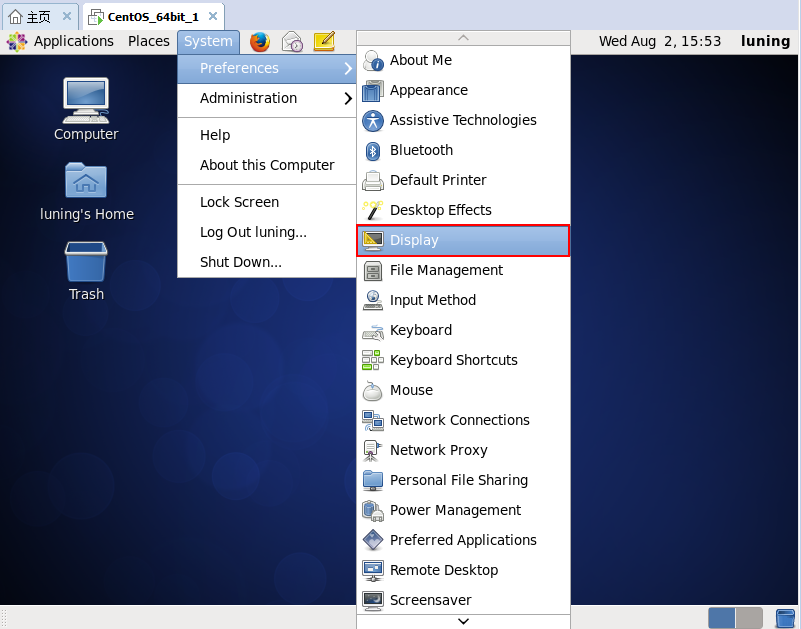
2，更换桌面背景

进入下面菜单。

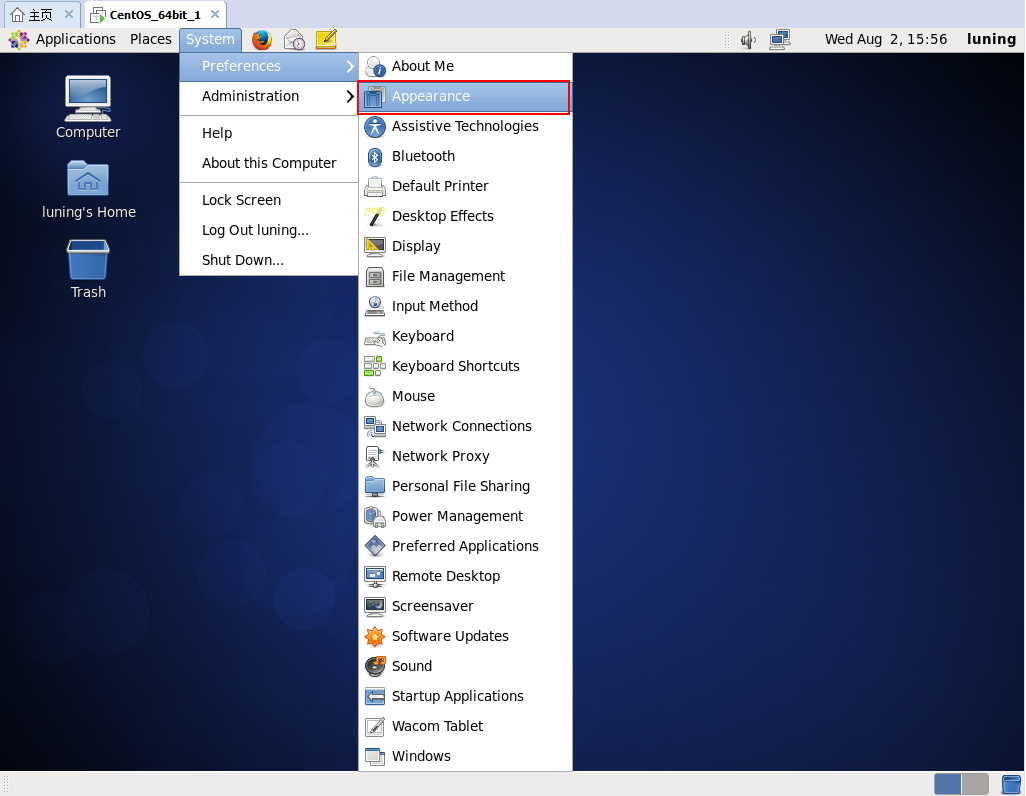
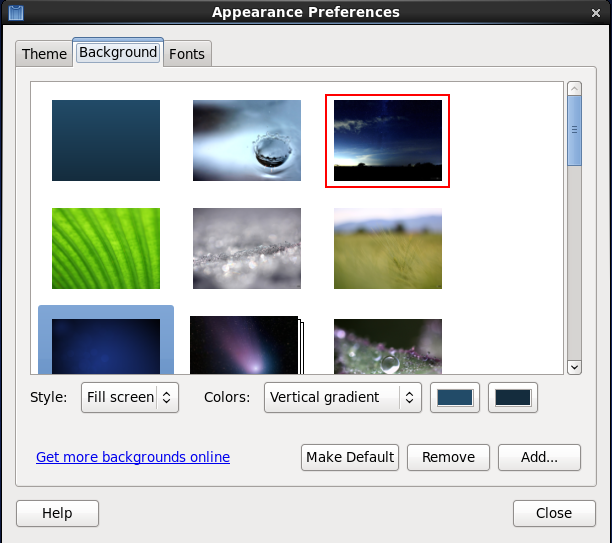
选择一张背景图片，然后点击OK。

3，更改窗口打开方式

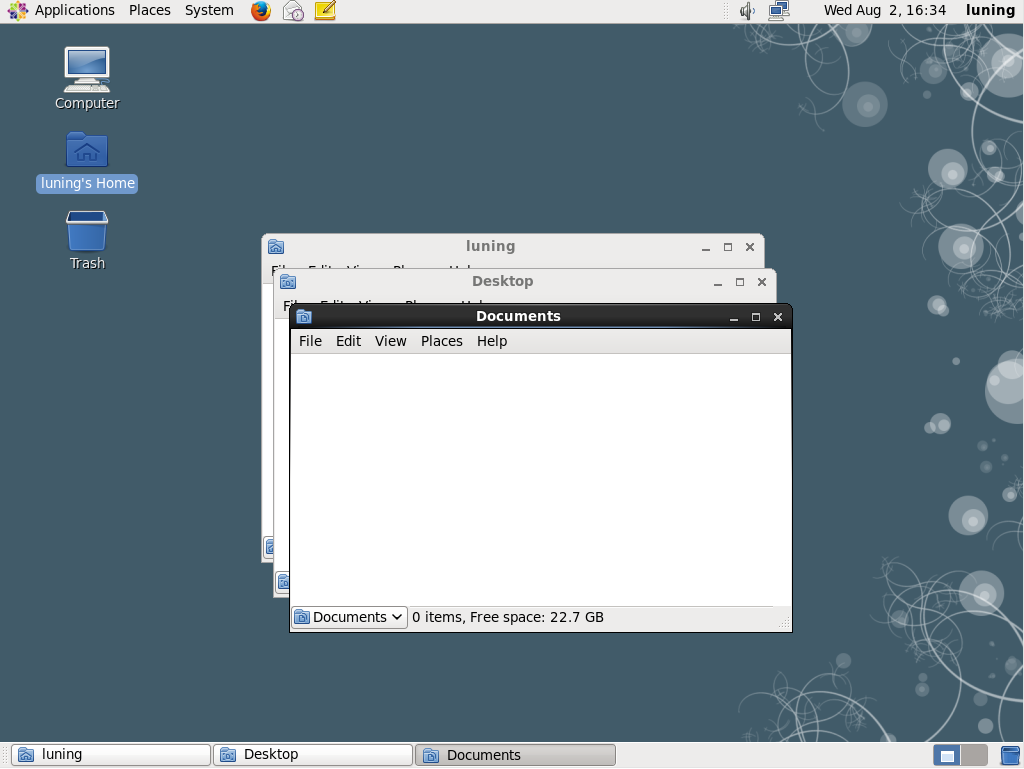
默认每次都打开一个新的窗口，这样看起来比较凌乱，如下图。

进入下面菜单，设置在同一个窗口中打开，如下图。

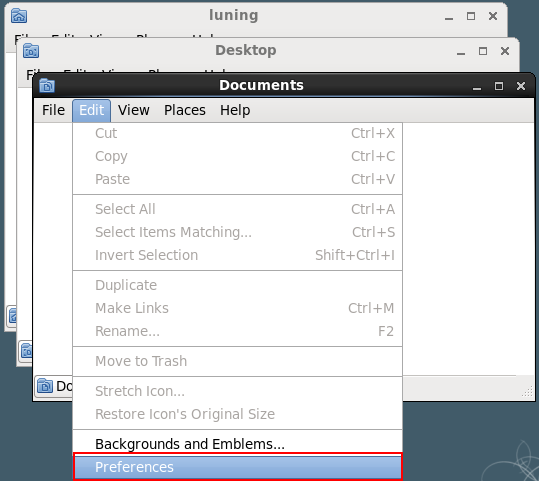
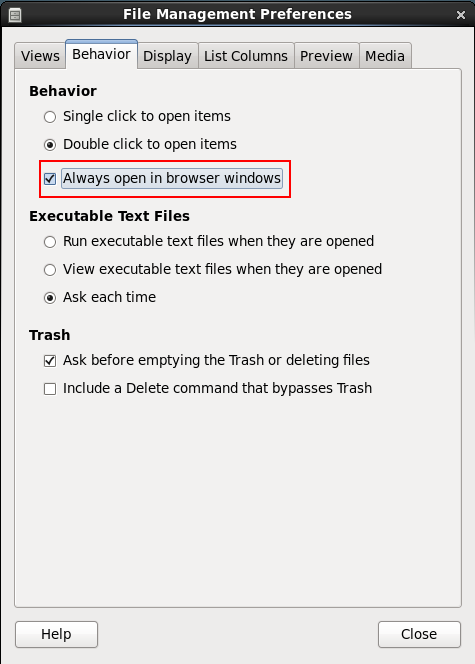
然后勾选如下选项，点击保存即可。

Terminal终端

 默认使用的是GNOME图形界面，但是学习Linux，一定要学会使用命令行，打开Terminal终端有两种方式。

方式一：在当前目录右键

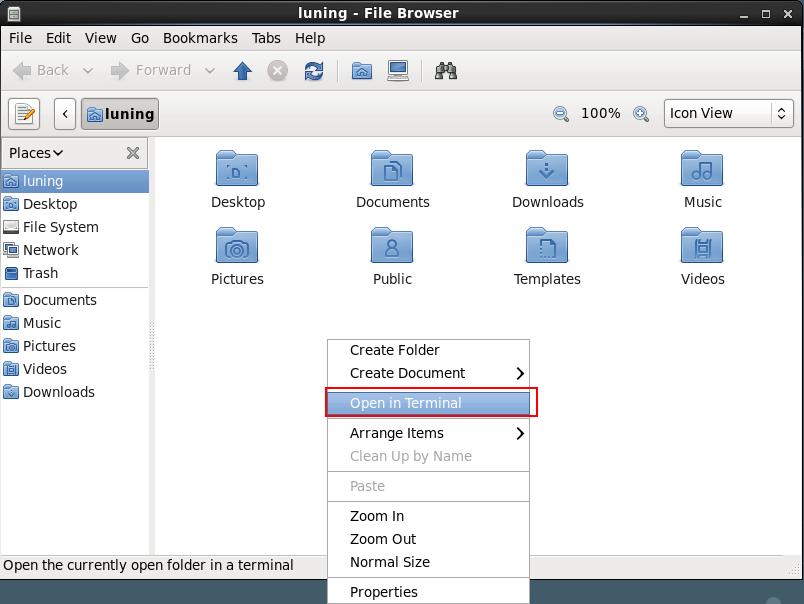
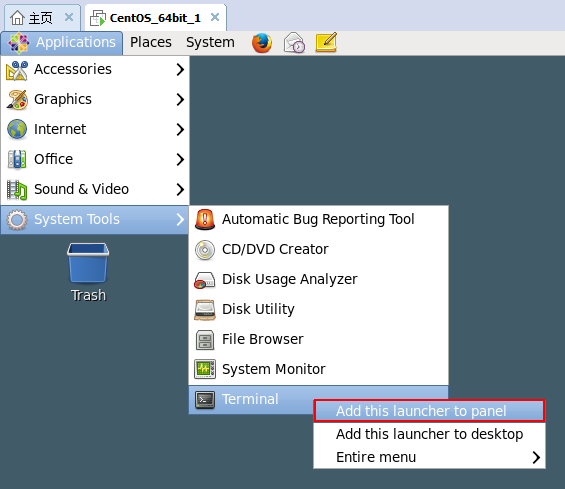
方式二：进入下面菜单，选择Terminal。

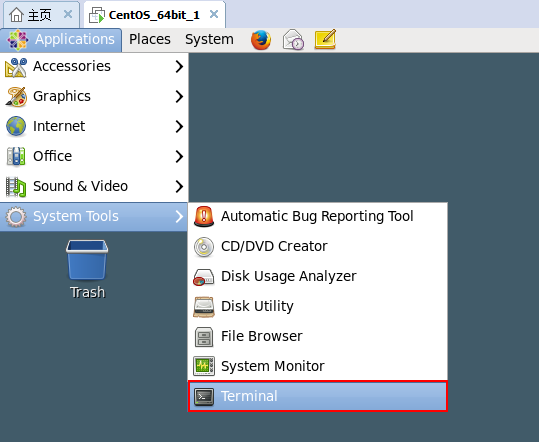
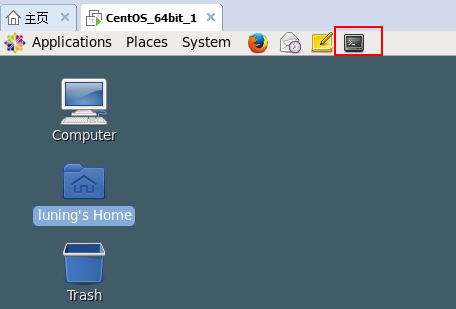
小技巧：我们可以把Terminal工具固定到工具栏中，如下图。

Workspace工作桌面

CentOS为我们提供了Workspace的概念，当我们需要多个桌面，而且每个桌面做不同的事情的时候，就可以充分利用Workspace了。

默认是有两个Workspace。

我们也可以右键，增加Workspace。

锁定，注销和关机

1，锁定

当我们临时要离开座位了，但是又不想别人操作我的电脑，就可以使用锁定功能了。有两个入口可以实现。

方法一：通过System菜单

如下图

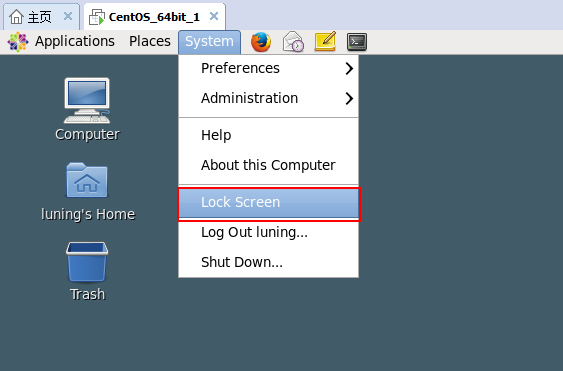
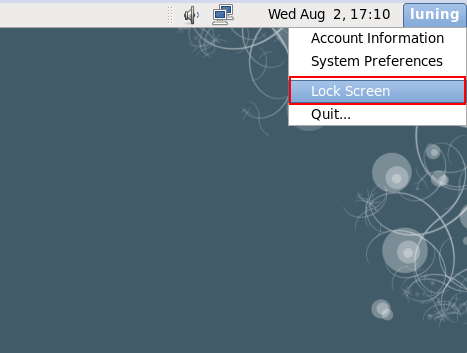
方法二：通过点击右上角的用户名，然后选择Lock Screen。

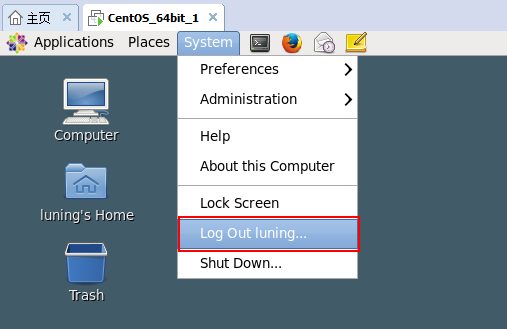
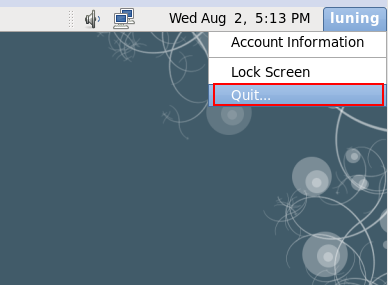
2，注销

当我们需要切换用户的时候，会选择注销。

同样有两个方式。

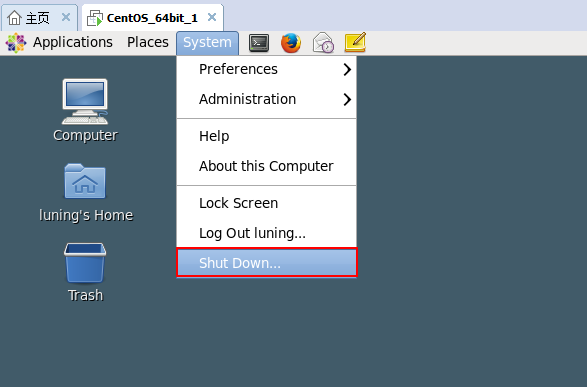
3，关机

总结

1. 尽量使用普通用户，而不要使用root用户，因为root有至高无上的权限，误操作会损坏系统。
2. 尽量使用命令行的方式而不是使用GNOME图形界面。