斐波那契求第n项

摘自  https://blog.csdn.net/lpjishu/article/details/51323116

斐波那契求第n项是常见的算法题

方法1  递归法

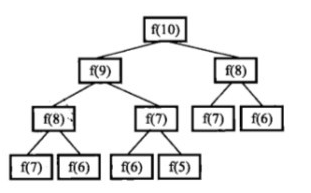
    //斐波那契 0,1,1,2,3,5  求n
    //调用过程像一个二叉树
    //f8 会调 f7,f6  f7会调用 f6,f5。 这样f6就重复了
    //45之后就很慢了
    function getN(n){
        if(n <= 0){
            return 0;
        }
        if(n === 1){
            return 1;
        }
        return getN(n - 1) + getN(n - 2);
    }
    console.log(getN(47));

方法2 循环

    //循环 秒出
    function getN(n){
        if(n <= 0){
            return 0;
        }
        if(n === 1){
            return 1;
        }
        var prev = 0;
        var next = 1;
        var num = 0;
        for (var i = 2; i <= n; i++) {
            num = next + prev
            prev = next
            next = num
        }
        return num;
    }
    console.log(getN(10000));