二叉树的创建、遍历(递归和非递归实现）、交换左右子数、求高度(c++实现)

要求：以左右孩子表示法实现链式方式存储的二叉树（lson—rson），以菜单方式设计并完成功能任务：建立并存储树、输出前序遍历结果、输出中序遍历结果、输出后序遍历结果、交换左右子树、统计高度，其中对于中序、后序的遍历运算要求采用非递归的方式实现。

写在前面

二叉树向量存储的优势和弊端

　　二叉树同样有两种存储方式，数组和链式存储，对于数组来说，我们利用二叉树的性质然后利用下标可以方便的找到一个节点的子节点和父节点。

　　　　

　　

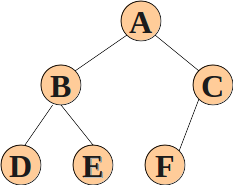
二叉树的性质:
　　1.二叉树的第i层上至多有2i-1个节点
　　2.深度为K的二叉树至多有2k-1个节点
　　3.任何一个二叉树中度数为2的节点的个数必度数为0的节点数目少1.
　　　　说明:度数为0,为叶子节点。
　　4.具有n个节点的完全二叉树的深度为|_Log2N_|+1
　　5.若完全二叉树中的某节点编号为i，则若有左孩子编号为2i，若有右孩子编号为2i+1，母亲节点为i/2。

　　结合第5条性质:

　　　　若完全二叉树中的某节点编号为i，则若有左孩子编号为2i，若有右孩子编号为2i+1，母亲节点为i/2。

　　可以在这种完全二叉树中十分方便的找到任何相关联(父子、兄弟等)的元素。

　　但是由于顺序存储天生适配于完全二叉树，对于下面这种非完全二叉树并不合适，主要体现在空间上的浪费，所以我们需要用到另一种存储方式——链式存储。

　　　

　

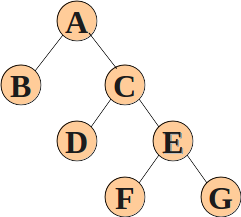
二叉树的链表存储

　　在链式存储中，每个节点的结构如下

　　

结构描述：

　　一个存储数据的变量与两个指向孩子的指针域。

　　利用指针域我们便可以完美的存储非完全二叉树，如下：

　　　

代码分解：

1.定义结构体变量，其中的tag只会在后序遍历（非递归）过程中使用。

typedef struct node{
	int tag;    //在后序遍历过程中来标志一个结点是第一次访问（tag=0）还是第二次访问（tag=1）
	int data;
	struct node* lson;
	struct node* rson;
}Bitree;
typedef Bitree* Bitpo;

2.创建二叉树。创建二叉树的方式有3种（前序、中序、后序），其过程与二叉树的遍历类似，这里我用前序来创建二叉树。

void create(Bitpo &T){                    //创建并存储二叉树,以先序顺序输入并存储（递归）
	int x;
	cin>>x;
	if(x==0)                              //'0'表示空节点
		T=NULL;
	else{
		T=(Bitpo)malloc(Len);
		T->data=x;
		create(T->lson);
		create(T->rson);
	}
}

3.前序遍历二叉树（递归）。

void pretraversal(Bitpo T){              //先序遍历（递归）
	if(T){
		cout<<T->data<<" ";
		pretraversal(T->lson);
		pretraversal(T->rson);
	}
}

4.中序遍历二叉树（非递归）。这里用数组模拟栈，用一个整型变量模拟栈顶指针，需要回溯。

void intraversal(Bitpo T){               //中序遍历（非递归）
	Bitpo stack[101];                    //定义栈并初始化
	Bitpo Q=T;
	int p=0;                             //初始化栈顶指针
	do{
		while(Q!=NULL){                  //遍历左子树
			p++;
			if(p==101){
				cout<<"Error:stack is full!!";
				return;                  //栈满,返回0
			}
			stack[p]=Q;                  //入栈，从下标1开始
			Q=Q->lson;
		}
		if(p!=0){
			Q=stack[p];
			p--;                         //退栈
			cout<<Q->data<<" ";          //访问根节点
			Q=Q->rson;                   //遍历右子树
		}
	}while(p!=0||Q!=NULL);
}

5.后序遍历二叉树（非递归）。同样的用数组模拟栈，用一个整型变量模拟栈顶指针，需要回溯和设立标志tag（已在结构体中定义），因为根节点最后一个访问，所以入栈时令tag=0入栈，第一次回溯出栈时令tag=1，重新入栈，第二次回溯出栈时才可以访问。

void posttraversal(Bitpo T){             //后序遍历（非递归）
	Bitpo stack[101];		 //定义栈并初始化
	int p=0;		         //初始化栈顶指针
	Bitpo Q=T;
	do{
		while(Q!=NULL){
			p++;
			if(p==101){      //栈满，退出
				cout<<"Error:stack is full!!";
				return;
			}
			Q->tag=0;        //第一次入栈，tag=0
			stack[p]=Q;	 //入栈
			Q=Q->lson;
		}
		if(p!=0){
			Q=stack[p];
			p--;             //退栈
			if(Q->tag==0){	 //第一次访问，令tag=1,重新入栈
				Q->tag=1;
				p++;
				stack[p]=Q;
				Q=Q->rson;//继续搜索Q的右子树
			}
			else{             //第二次入栈，访问Q结点，并且为了回溯，令Q=NULL
				cout<<Q->data<<" ";
				Q=NULL;
			}
		}
	}while(p!=0||Q!=NULL);
}

6.交换左右子树（递归）。

void exchange(Bitpo T){                  //交换左右子树（递归）
	if(T){
		Bitpo x=T->lson;
		T->lson=T->rson;
		T->rson=x;
		exchange(T->lson);
		exchange(T->rson);
	}
}

7.求二叉树的高度（递归）。

int height(Bitpo T){                     //求高度（递归）
	if(T){
		return 1+max(height(T->lson),height(T->rson));
	}
	else
		return 0;
}

8.主函数如下。

int main(){
	int q=1;
	Bitpo root;
	while(q){
		cout<<"1.create and store binary tree!"<<endl;
		cout<<"2.travel in preorder!"<<endl;
		cout<<"3.travel in inorder!"<<endl;
		cout<<"4.travel in postorder!"<<endl;
		cout<<"5.change lson and rson!"<<endl;
		cout<<"6.calculate the height of the tree!"<<endl;
		cout<<"0.exit!"<<endl;
		cin>>q;
		switch(q){
			case 0:
				q=0;
				break;
			case 1:
				create(root);
				cout<<endl<<"create successfully!"<<endl<<endl;
				break;
			case 2:
				cout<<"preorder:";
				pretraversal(root);
				cout<<endl<<endl;
				break;
			case 3:
				cout<<"inorder:";
				intraversal(root);
				cout<<endl<<endl;
				break;
			case 4:
				cout<<"postorder:";
				posttraversal(root);
				cout<<endl<<endl;
				break;
			case 5:
				exchange(root);
				cout<<"exchange successfully!!"<<endl<<endl;
				break;
			case 6:
				cout<<"height:"<<height(root)<<endl<<endl;
				break;
		}
	}
	return 0;
}