关于graham扫描法求凸包的小记

1、首先，凸包是啥：

若是在二维平面上，则一般的，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，它能包含点集中所有的点。

───────────────────────────────────────────────────────────────────────────────────────────────────────────

2、那么，如何通过某种算法求二维平面上的凸包呢？

有Graham扫描法（Graham scan algorithm），复杂度O(nlogn)。

话不多说，先上当年大佬的论文……

呃，可以看到，这个标题是非常的酷嗷，对于有限平面点集的凸包计算的高效算法，划重点。

给一个平面点集S，标号为s₁~s_n，据说我们经常对找它的凸包感兴趣（真的吗……我怎么从来没感兴趣过……）

然后graham教授就给了我们一种炫酷的五步法，来求凸包。

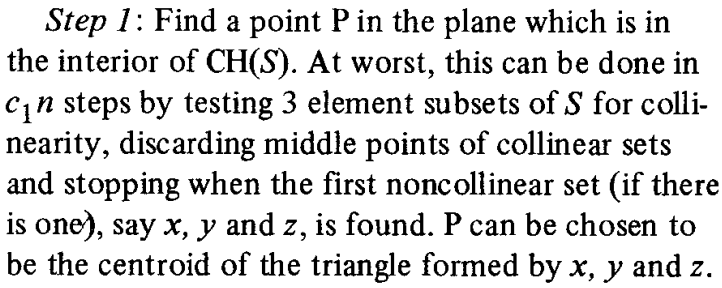
第一步：

　　目标是找个在凸包内部的点P。

　　我们对集合S三个点三个点进行检测，检测它们是否共线：

　　　　若共线，扔掉中点；

　　　　若不共线，就选这三个点所组成的三角形的质心作为点P。

第二步：

　　以P为原点，任意一个方向为θ=0轴，建立一个极坐标系；

　　对集合S中的每个点s_i，都按这个坐标系表示一下它们的坐标。

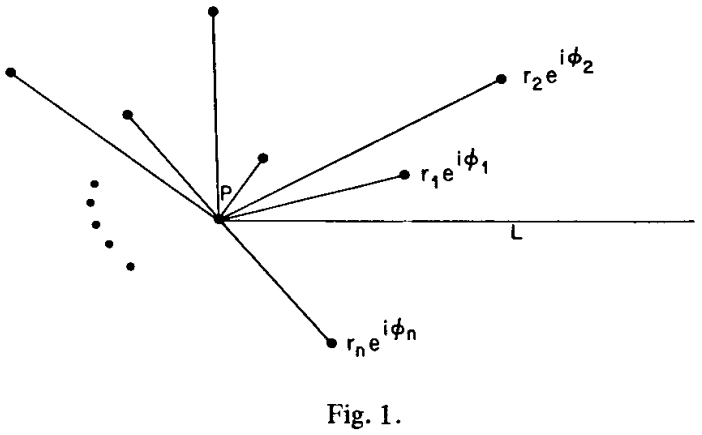
第三步：

　　现在每个点都有坐标 r _i ∠ θ _i ，我们对这些点，按照θ的升序进行排序。

第四步：

　　如果有某两个点的角度相等，就删掉r较小的那个点，因为它显然不可能是凸包边界上的点。

　　另外呢，所有r=0的，也可以删了，反正也impossible。

　　then，重新给还存在着的点编号，新的集合记为S'。

           

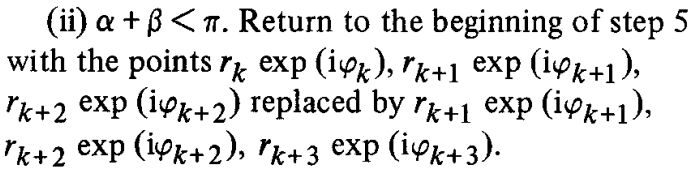
第五步：

　　对于S'中连续的三个点k,k+1,k+2，如图2，有两种可能：

　　　　1）α + β ≥ π，看图，就很容易知道，这个点k+1，显然不可能是凸包边界上的点了；

　　　　　　回到步骤五，重新选择点k-1,k,k+2作为新的三个点；

　　　　2）α + β < π，就回到步骤五，选择点k+1,k+2,k+3作为新的三个点；

　　　　　　相当于往前进。

原文件：https://files.cnblogs.com/files/dilthey/graham%E6%89%AB%E6%8F%8F%E6%B3%95.pdf

───────────────────────────────────────────────────────────────────────────────────────────────────────────

3、那么放到程序中，具体如何实现呢？

我们保留“对于三个点，判断角α、β和是否小于180度，并且进行相应的前进退后”的思想，不过对于选取原点的方法进行一定的修改。

　　①找到点集S中纵坐标最小的点（如果y坐标相同，则选其中横坐标最小的），作为原点P₀。

　　②计算其他所有点的辐角，并且将他们按从小到大排序，如果遇到辐角相同的一些点，则按与原点距离从小到大排序，记为P₁~P_n。

　　③建栈，入栈P₀,P₁,P₂；

　　④选取一个点P_i（i初始值为3），前往步骤⑤；

　　⑥获得栈顶点和次栈顶点P_k,P_k-1，

　　　　进行判定：如果 P_k-1 -> P_k -> P_i 是右转的（其实就是α + β ≥ π），就弹出栈顶元素，并且返回步骤⑥；

　　　　　　　　　如果是左转的（α + β < π），就入栈点P_i，并且i+=1，返回步骤④；

───────────────────────────────────────────────────────────────────────────────────────────────────────────

4、代码模板：

#include<bits/stdc++.h>
#define MAX 10005
#define eps 1e-6
using namespace std;
struct Point{
    double x,y;
    Point(double tx=,double ty=):x(tx),y(ty){}
}p[MAX];
typedef Point Vctor;
Vctor operator - (Point A,Point B){return Vctor(A.x-B.x,A.y-B.y);}
int dcmp(double x)
{
    if(fabs(x)<eps) return ;
    else return (x<)?(-):();
}
//叉积
double Cross(Vctor A,Vctor B){return A.x*B.y-A.y*B.x;}
//距离
double dist(Point p1,Point p2){return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));}
bool cmp(Point p1,Point p2)
{
    double tmp=Cross(p1-p[],p2-p[]);
    if(!dcmp(tmp)) return dist(p[],p1)<dist(p[],p2);
    else return tmp>;
}
vector<Point> graham_scan(int n)
{
    vector<Point> ans;

    if(n<=) return ans;
    if(n<=)//当只有1或2个点时
    {
        if(n== && (p[].y<p[].y || (p[].y == p[].y && p[].x < p[].x)) ) swap(p[],p[]);
        for(int i=;i<n;i++) ans.push_back(p[i]);
        return ans;
    }

    int idx=;
    for(int i=;i<n;i++)//选出Y坐标最小的点，若Y坐标相等，选择X坐标小的点
    {
        if(p[i].y<p[idx].y || (p[i].y == p[idx].y && p[i].x < p[idx].x)) idx=i;
    }
    swap(p[],p[idx]);
    sort(p+,p+n,cmp);
    for(int i=;i<=;i++) ans.push_back(p[i]);
    int top=;
    for(int i=;i<n;i++)
    {
        while(top> && Cross(p[i]-ans[top-],ans[top]-ans[top-]) >= )
        {
            ans.pop_back();
            top--;
        }
        ans.push_back(p[i]);
        top++;
    }
    return ans;
}