POJ 2914 - Minimum Cut - [stoer-wagner算法讲解/模板]

首先是当年stoer和wagner两位大佬发表的关于这个算法的论文：A Simple Min-Cut Algorithm

直接上算法部分：

　　　　　　　　　　　　　　　　　　　　　　　　　　分割线　　　　　　　　　　　　　　　　　　　　　　　　　　begin

在这整篇论文中，我们假设一个普通无向图G=(V,E)，其中每条边e都有一个正实数权值w(e)。

　　如果我们知道：怎样找到两个节点s,t，以及怎样得到对于s-t的最小割，我们就几乎解决了整个问题：

　　定理2.1：

　　　　设s和t是图G中的两个节点，设G/{s,t}是合并s和t后得到的图，

　　　　则图G的全局最小割可以通过“图G对于s-t的最小割”和“图G/{s,t}的全局最小割”得到。

定理说明：

　　若图G存在一个全局最小割，使得s和t被分割，那么，图G的s-t最小割就等于图G的全局最小割。

　　否则（即全局最小割没有分割s和t），图G的全局最小割就等于图G/{s,t}的全局最小割。

因此，我们可以使用一个寻找任意s-t最小割的程序来构建一个递归算法，从而寻找一个图的全局最小割。

下面的算法（使用一些骚操作搜索方法），可以产生我们想得到的s-t最小割。

MinimumCutPhase(G,w,a)  //分阶段(phase)，每个阶段都产生相应的当前阶段最小割

{

　　A←{a}

　　while( A ≠ V )

　　{

　　　　选取“最紧密相连的点”加入A

　　}

　　记录当前阶段的割，并且合并最后加入的两个点

}

呵，听起来就很玄乎，什么玩意儿呢，下面有解释。

A是作为V的一个子集，开始时是空集，我们任取一个点，加入到A中，然后通过某个规则不断地往A中加入点，直到A == V为止，那是什么规则呢？

　　在每一步的加点操作中，我们选择集合(V - A)中和A“最紧密相连的点”加入A，那什么是“最紧密相连的点”呢？

　　　　设：点y∈ V - A ，且点y为与集合A直接相连的点，所有点y的集合为Y；

　　　　　　所有与集合A直接相连的边的权重总和为w(A,y)；

　　　　则：“最紧密相连的点” z 满足： z ∈ Y，并且w(A,z)为所有w(A,y)中最大的。

　　　　通俗的说，就是V - A集合里，找一个直接与A相连的点，这个点是 Σ(该点所有与A直接相连的边的权值) 最大的那个。

（不难看出，这是一种类似于prim算法生成类似最大生成树的算法）

在我们不断往A加点的过程中，记录下最后加入A的两个点，记为s和t，对这两个点进行合并操作(merge)：

　　删除点s和点t，加入新的点u作为代替，所有原本从s或t点出发的边（edge< s , t >除外，这条边删除；并且设这些边到达的点为x），都用一条新的edge< u , x >代替；

　　并且　edge< u , x >.weight　=　edge< s , x >.weight　+　edge< t , x >.weight　;　 (若某条边不存在，则定义其weight=0)

　　（当然需要注意的是，所有讨论都是建立在无向图上，故这里的出发、到达不代表这条边的方向，只是单纯描述该边的两个端点）

然后，我们把当前分割s和t的割（cut），叫做阶段割（the-cut-of-phase），不难得到，阶段割等于w(A,t) （注意，此处的集合A表示加入点t前的集合A）；

then，所有阶段割中最小的，即本算法的结果，即我们想求的全局最小割。

MinimumCut(G,w,a)

{

　　while(|V| > 1)

　　{

　　　　MinimumCutPhase(G,w,a)

　　　　if(阶段割 < 当前全局最小割) 当前全局最小割 = 阶段割

　　}

}

最后，注意到节点a在本算法整个过程中是一直不变的，实际上它也可以在每个阶段(phase)进行任意选择。

　　　　　　　　　　　　　　　　　　　　　　　　　　　分割线　　　　　　　　　　　　　　　　　　　　　　　　　　end

然后是论文中的example部分：

　　　　　　　　　　　　　　　　　　　　　　　　　　　分割线　　　　　　　　　　　　　　　　　　　　　　　　　　begin

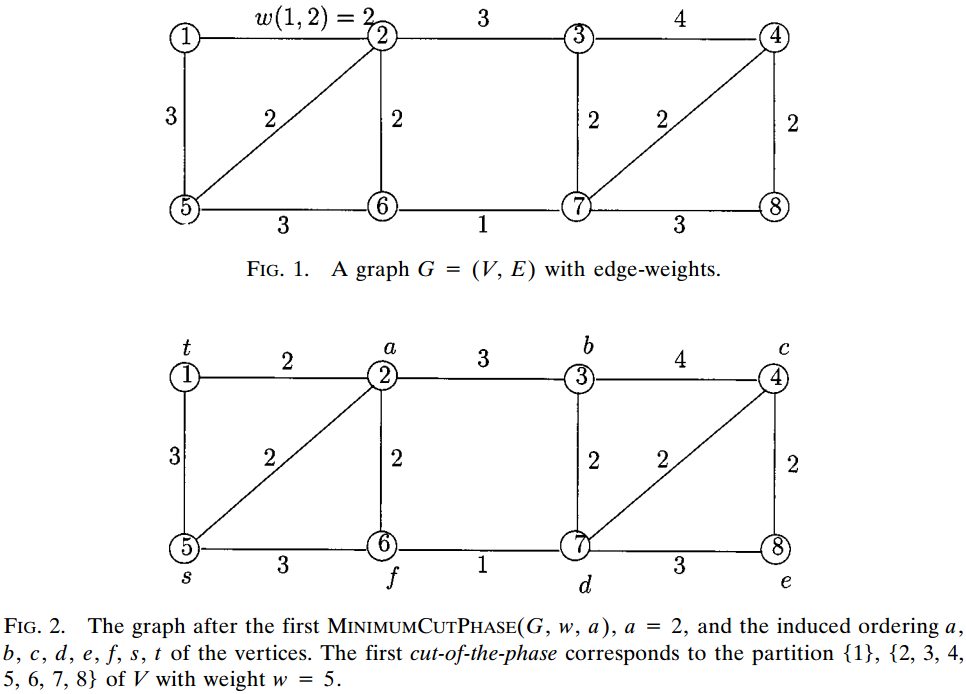
这是第一次MinimumCutPhase(G,w,a)操作前和操作后的样子，

在此次MinimumCutPhase(G,w,a)操作中，进入集合A的点的顺序为: 2 → 3 → 4 → 7 → 8 → 6 → 5(s) → 1(t) ；

显然，此次的阶段割cut-of-the-phase.weight = w(A,t) = edge<1,2>.w + edge<1,5>.w = 5 ；

之后的操作与此类似，不再赘述，可以自行对照论文中的FIG。

　　　　　　　　　　　　　　　　　　　　　　　　　　　分割线　　　　　　　　　　　　　　　　　　　　　　　　　　end

当然，上stoer和wagner两位巨老当初的论文，装逼成分多余实际效用= =，感觉自己翻译也翻译的像一坨shit一样；

更多细节更深理解还请看中文：http://files.cnblogs.com/files/dilthey/stoer-wagner%E7%AE%97%E6%B3%95.pdf

先上算法模板以及解释：

 #include<cstring>
 #define MAXN 505
 #define INF 0x3f3f3f3f
 int n,m;//n个点,m条边
 int edge[MAXN][MAXN],dist[MAXN];
 bool vis[MAXN],bin[MAXN];
 void init()
 {
     memset(edge,,sizeof(edge));
     memset(bin,,sizeof(bin));
 }
 int merge(int &s,int &t)//对应论文中的MinimumCutPhase()
 {
     memset(dist,,sizeof(dist));
     memset(vis,,sizeof(vis));
     int k,mincut,maxc;
     for(int i=;i<=n;i++)
     {
         k=-, maxc=-;
         for(int j=;j<=n;j++) if(!bin[j] && !vis[j] && dist[j] > maxc) {k=j;maxc=dist[j];}
             //寻找"the most tightly connected vertex"
         if(k == -) return mincut;
         vis[k]=true;//点k加入集合A
         s=t; t=k;//不断移动s和t,保证他们是最后进入集合A的两个点
         mincut=maxc;//不断更新mincut为w(A,t)
         for(int j=;j<=n;j++) if(!bin[j] && !vis[j]) dist[j]+=edge[k][j];//计算所有的w(A,y)
     }
     return mincut;
 }
 int stoer_wagner()
 {
     int mincut=INF,s,t,ans;
     for(int i=;i<=n-;i++)//merge(s,t)一次减少一个点,|V|要从n减少到1,故要进行n-1次
     {
         ans=merge(s,t);
         bin[t]=;//把t合并到s中
         if(ans<mincut) mincut=ans;
         if(mincut==) return ;
         for(int j=;j<=n;j++) if(!bin[j]) edge[s][j]=(edge[j][s]+=edge[j][t]);//更新所有从s出发的边
     }
     return mincut;
 }

时间复杂度O(n³)；

再说POJ2914，

题目链接：http://poj.org/problem?id=2914

有了模板之后，就是模板题；

当然，需要注意的是，这道题目里，n个点标号是0~n-1，用这个模板的话需要在输入的时候自己+1；

另外，这道题目的输入有重边，所以存边的时候，使用“+=”，而不是“=”；

 #include<cstdio>
 #include<cstring>
 #define MAXN 505
 #define MAXM MAXN*MAXN/2
 #define INF 0x3f3f3f3f
 using namespace std;
 int n,m;
 int edge[MAXN][MAXN],dist[MAXN];
 bool vis[MAXN],bin[MAXN];
 void init()
 {
     memset(edge,,sizeof(edge));
     memset(bin,,sizeof(bin));
 }
 int merge(int &s,int &t)
 {
     memset(dist,,sizeof(dist));
     memset(vis,,sizeof(vis));
     int k,mincut,maxc;
     for(int i=;i<=n;i++)
     {
         k=-, maxc=-;
         for(int j=;j<=n;j++) if(!bin[j] && !vis[j] && dist[j] > maxc) {k=j;maxc=dist[j];}
         if(k == -) return mincut;
         vis[k]=true;
         s=t; t=k;
         mincut=maxc;
         for(int j=;j<=n;j++) if(!bin[j] && !vis[j]) dist[j]+=edge[k][j];
     }
     return mincut;
 }
 int stoer_wagner()
 {
     int mincut=INF,s,t,ans;
     for(int i=;i<=n-;i++)
     {
         ans=merge(s,t);
         bin[t]=;
         if(ans<mincut) mincut=ans;
         if(mincut==) return ;
         for(int j=;j<=n;j++) if(!bin[j]) edge[s][j]=(edge[j][s]+=edge[j][t]);
     }
     return mincut;
 }
 int main()
 {
     while(scanf("%d%d",&n,&m)!=EOF)
     {
         init();
         for(int i=;i<=m;i++)
         {
             int a,b,c;
             scanf("%d%d%d",&a,&b,&c);
             edge[a+][b+]+=c;
             edge[b+][a+]+=c;
         }
         printf("%d\n",stoer_wagner());
     }
 }