支撑矢量机SVM

1.线性SVM

首先，回顾一下SVM问题的定义，如下：

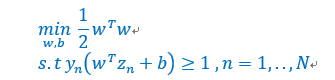
线性约束很烦，不方便优化，是否有一种方法可以将线性约束放到优化问题本身，这样就可以无拘无束的优化，而不用考虑线性约束了。其对应的拉格朗日对偶形式为：

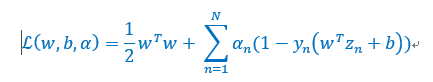
最终的优化结果保证离超平面远的点的权重为0。

经过上面的对偶变化，下面来一步一步的简化我们的原始问题，

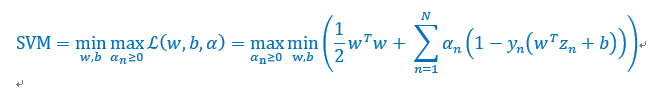
首先对b求偏导数,并且为0：

对w求偏导数：

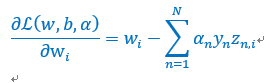也就是

化简原型

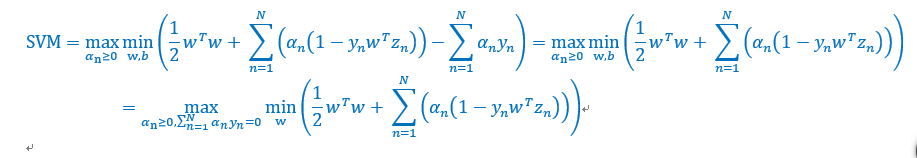
将w带入，并且去掉min，得到如下

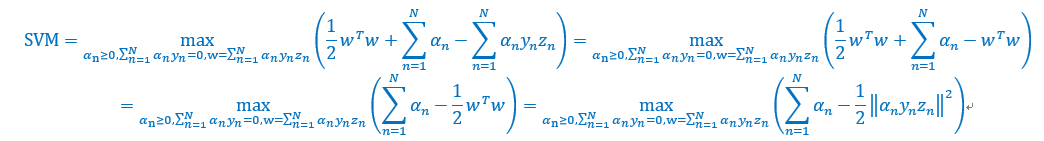
执行到这里，现在目标函数只与有关，形式满足QP，可以轻易得到，也就是得到w。但是在计算过程中，需要计算一个中间矩阵Q，维度为N*N，这个是主要计算开销。上一讲无需计算这个Q，因为Q的形式十分简单。

计算出拉格朗日乘子就得到了w：

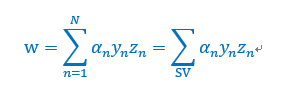
而对于b的计算，KT条件帮助我们解决这个问题。如果原始问题和对偶问题都有最优解，且解相同，那么会满足KKT条件。这也是一个充分必要条件，其中很重要的一点是complementary
slackness(互补松弛性)，该条件有下面等式成立，

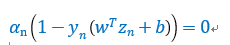
由于（对偶条件），且（原始条件），那么两者有一个不为0时，另外一个必然为0。所以，只要找到一个，就可以利用这个性质计算出b，计算方

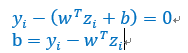
理论来说，只需要一个点就可以，但是实际上由于计算有误差，可能会计算所有的b，然后求平均。并且这些可以计算出b的点，就是支持向量，因为他们满足了原始问题中支撑向量的定义。但是，并不是所有的支撑向量，都有对应的。一般的，我们只用的向量称为支撑向量：

或者，b这样计算：

2.非线性SVM

对于数据不可分的情况，使用核空间映射方法。即将线性不可分，映射到高维度空间，变为线性可分。在线性不可分的情况下，支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开。

本质上，不知道非线性核映射的具体形式。实际上需要的也只是两个向量在核映射后的内积值而已。常使用的核函数包括SVM核函数。同时，对于新样本，也并未实际需要计算出w。如分类函数所示

3.带松弛变量的SVM

通常，高维数据本身是非线性结构的，而只是因为数据有噪音。经常存在偏离正常位置很远的数据点，我们称之为 outlier ，在我们原来的 SVM 模型里，outlier 的存在有可能造成很大的影响，因为超平面本身就是只有少数几个 support vector 组成的，如果这些 support
vector 里又存在 outlier 的话，其影响就很大了。

松弛变量定义了一个常量，即对于每个支撑样本，容许他距离超平面的距离在1的一定范围内波动，即：

C为松弛系数或者惩罚因子，优化目标方程变为：

其中 C是一个参数，用于控制目标函数中（“寻找margin最大的超平面”和“保证数据点偏差量最小”）之间的权重。注意，其中
ξ 是需要优化的变量（之一），而C是一个事先确定好的常量。对应的拉格朗日对偶形式为：

   

         即整个过程中，只不过计算的拉格朗日乘子alpha多了一个上限。

     （1）并非所有的样本点都有一个松弛变量与其对应。实际上只有“离群点”才有，或者也可以这么看，所有没离群的点松弛变量都等于0。

     （2）松弛变量的值实际上标示出了对应的点到底离群有多远，值越大，点就越远。

     （3）惩罚因子C决定了你有多重视离群点带来的损失，显然当所有离群点的松弛变量的和一定时，你定的C越大，对目标函数的损失也越大，此时就暗示着你非常不愿意放弃这些离群点，即希望松弛变量越小越好。最极端的情况是你把C定为无限大，这样只要稍有一个点离群，目标函数的值马上变成无限大，马上让问题变成无解，这就退化成了硬间隔问题。

     （4）惩罚因子C不是一个变量，整个优化问题在解的时候，C是一个你必须事先指定的值。

         松弛变量也有变形形式。例如用来解决分类问题中样本的“偏斜”问题。先来说说样本的偏斜问题，也叫数据集偏斜（unbalanced），它指的是参与分类的两个类别（也可以指多个类别）样本数量差异很大。

         对于SVM。假设正样本明显多于负样本，会导致分类超平面往负样本偏移。对于此种情况，可以给负样本较大的惩罚因子，对应正样本小一点的惩罚因子。

          LibSvm即使用此种方式调节，实际过程中。libSVM就直接使用样本数量的比来作为正负样本的惩罚因子。

          SVM方法，在经验误差和推广误差方面达到平衡。但是在大样本上存在较大的计算代价，此时可以使用样本抽样来解决。对于多分类问题，则存在死区。

参考：

1.机器学习基石--学习笔记02--Hard Dual SVM

2.SVM学习（五）：松弛变量与惩罚因子

3.支持向量机通俗导论（理解SVM的三层境界）

4.机器学习算法与Python实践之（二）支持向量机（SVM）初