P1959 遗址_NOI导刊2009普及（6）

题意：平面上n个点（坐标$0\le x,y\le 5000，n \le 3000$）

　　　求以其中四个点为顶点的正方形的最大面积

$O(n^2)$枚举两个点作为当前正方形的对角线

那么如何求出另外两个点呢？

设一个点为$（ax，ay）$，另一个为$（bx，by）$

所求点$（cx，cy），（dx，dy）$

考虑正方形中点$(\frac{ax+bx}{2},\frac{ay+by}{2})$

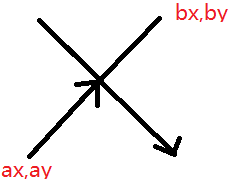
可以求出左边的向量为$(\frac{bx-ax}{2},\frac{by-ay}{2})$

右边的向量等于左边的向量旋转（自己举例推）$(\frac{by-ay}{2},\frac{ax-bx}{2})$

于是，右下角的点的坐标等于中点加右边的向量

　　　左上角点的坐标等于中点减右边的向量

如果那两个点是小数，是不成立的

怎么判断呢？

可以发现，那两个点的结果是由ax，ay，bx，by通过加加减减之后除以二得到的，

也就是说ax，ay，bx，by通过加加减减得到的应该是偶数

因此ax，ay，bx，by中必须要有偶数个奇数才成立！

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cctype>
#include<algorithm>
using namespace std;
#define olinr return
#define _ 0
#define love_nmr 0
#define DB double
inline int read()
{
    int x=,f=;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-')
            f=-f;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }
    return x*f;
}
inline void put(int x)
{
    if(x<)
    {
        x=-x;
        putchar('-');
    }
    if(x>)
        put(x/);
    putchar(x%+'');
}
int n;
struct node
{
    int x;
    int y;
}E[];
bool vis[][];
int ans;
double eps=1e-;
inline int ok(int i,int j)
{
    int ax=E[i].x;
    int ay=E[i].y;
    int bx=E[j].x;
    int by=E[j].y;
    if((ax^ay^bx^by)&) return -;  //判断是否有奇数个奇数
    int cx=(ax+bx+by-ay)>>;     //四个点的坐标
    int cy=(ay+by+ax-bx)>>;
    int dx=(ax+bx-by+ay)>>;
    int dy=(ay+by-ax+bx)>>;
    if(cx<||cy<||dx<||dy<||cx>||cy>||dx>||dy>||!vis[cx][cy]||!vis[dx][dy]) return -;  //没超范围并且点存在
    int fx=cx-ax;
    int fy=cy-ay;
    return fx*fx+fy*fy;   //面积
}
int main()
{
    n=read();
    for(int i=;i<=n;i++)
    {
        E[i].x=read();
        E[i].y=read();
        vis[E[i].x][E[i].y]=true;
    }
    for(int i=;i<=n;i++)
        for(int j=;j<=n;j++)
        {
            if(i==j) continue;
            ans=max(ans,ok(i,j));
        }
    put(ans);
    olinr ~~(^_^)+love_nmr;
}