hihoCoder #1143 : 骨牌覆盖问题·一 （斐波那契数列）

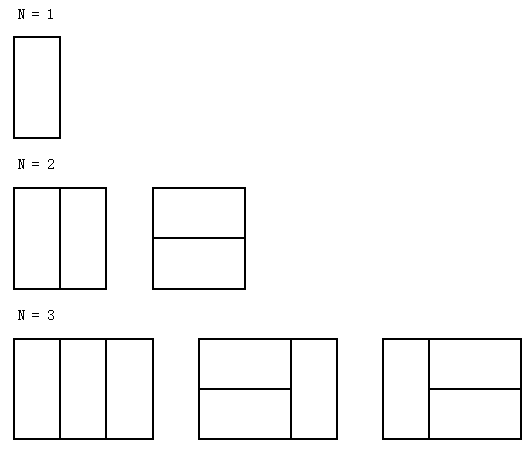
题意：我们有一个2xN的长条形棋盘，然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘，一共有多少种不同的覆盖方法呢？

思路：这是斐波那契数列啊，f[n] = f[n-1] + f[n-2]，初始时 f[0]=1,f[1]=1,f[2]=2。其实跟下面的递推思路差不多吧。但是关于这种简单，一般都可以用矩阵快速幂解决，即O(logn)时间内解决。主要难点是构造初始矩阵，如果是后面一个数字是由卡面两个数字相加而成的，那么一般可构造一个2*2的01矩阵，才这么小，随便试试吧，只要乘完的结果第二位是答案即可。

 #include <iostream>
 using namespace std;
 const int yu = ;
 const int MASK = ;
 struct fuf
 {
     long long a,b,    //矩阵如左
               c,d;
 }q[];

 int handle_it()
 {
     q[].a=; q[].b=; q[].c=; q[].d=;    //矩阵M的1次方
     int i=;
     for(; i<=; i++)    //作乘
     {
         q[i].a = ( q[i-].a * q[i-].a + q[i-].b * q[i-].c )%yu;
         q[i].b = ( q[i-].a * q[i-].b + q[i-].b * q[i-].d )%yu;
         q[i].c = ( q[i-].c * q[i-].a + q[i-].d * q[i-].c )%yu;
         q[i].d = ( q[i-].c * q[i-].b + q[i-].d * q[i-].d )%yu;
     }
     return ;
 }
 int main()
 {
     handle_it();
     int n;
     while( cin>>n )
     {
         if( n> && n<=)     {cout<<n<<endl;continue;}
         int i=;
         while( (n&MASK)== )        //直到n后面的0被去掉
         {
             i++;
             n >>= ;
         }
         fuf ans = q[i++];
         n >>= ;
         for( ; i< && n!=; i++,n >>= )
         {
             if( (n&)== )
             {
                 fuf tmp;
                 tmp.a = ( ans.a * q[i].a + ans.b * q[i].c )%yu;
                 tmp.b = ( ans.a * q[i].b + ans.b * q[i].d )%yu;
                 tmp.c = ( ans.c * q[i].a + ans.d * q[i].c )%yu;
                 tmp.d = ( ans.c * q[i].b + ans.d * q[i].d )%yu;
                 ans = tmp;
             }
         }
         cout<<ans.d<<endl;
     }
     return ;
 }

骨牌

　　写了个递推的思路：

　　（1）设dp[i]表示2*(i-1)的棋盘的摆放种数。

　　（2）假设第i列是放一个竖的，那么dp[i+1]+=dp[i]。这样只是一种，所以只是单纯用加的方式。

　　（3）假设第i列是放横的，那么连同第i+1列都被占用了，所以第i和i+1列就被摆放了两个横的，那么dp[i+2]+=dp[i]。这又是一种。

　　（4）2*n的棋盘答案就自然是dp[n+1]了，表示前n列的摆放种数。

 #include <bits/stdc++.h>
 #define pii pair<int,int>
 #define INF 0x3f3f3f3f
 #define LL long long
 using namespace std;
 const int N=1e8+;
 const int mod=;
 int dp[N], ans[N];
 void pre_cal()
 {
     dp[]=;
     for(int i=; i<N; i++)
     {
         dp[i+]=(dp[i+]+dp[i])%mod;    //考虑放横
         dp[i+]=(dp[i+]+dp[i])%mod;    //考虑放直
         ans[i]=(dp[i]+dp[i-])%mod;
     }
 }

 int main()
 {
     freopen("input.txt", "r", stdin);
     pre_cal();
     int  n;
     while(~scanf("%d",&n))    printf("%d\n",ans[n]);
     return ;
 }

TLE代码