maya2016无法安装卸载激活失败
AUTODESK系列软件着实令人头疼,安装失败之后不能完全卸载!!!(比如maya,cad,3dsmax等)。有时手动删除注册表重装之后还是会出现各种问题,每个版本的C++Runtime和.NET framework也是不同的,OMG!!!看了网上各种办法,都没有有效的解决方法。下面介绍如何借助一个工具完全卸载删除修复注册表,然后重装就OK了,另外还可以修复系统缺失或者损坏的组件,比如C++各种,.NET问题,显卡驱动问题,许可证问题。
1、如图所示,选择MAYA

2、如图所示,选择MAYA版本,比如2018
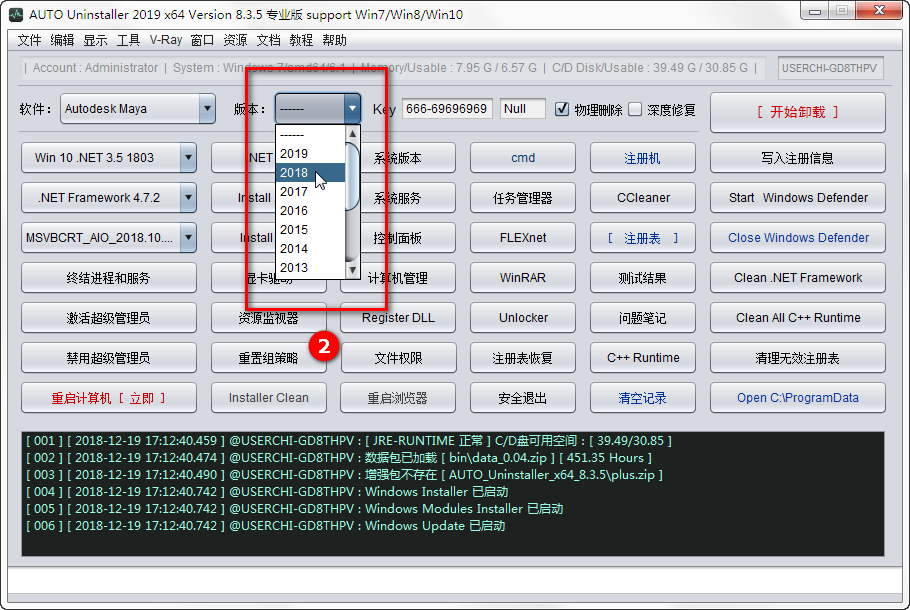
3、如图所示,点击【开始卸载】,然后重新安装
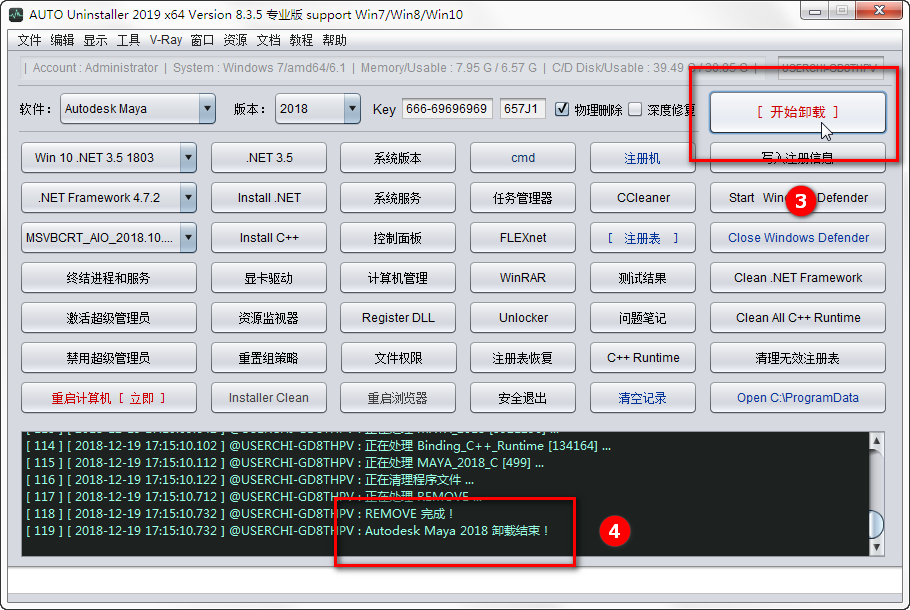
4、重新安装后可以使用了

maya2016无法安装卸载激活失败的更多相关文章
- maya2012无法安装卸载激活失败
AUTODESK系列软件着实令人头疼,安装失败之后不能完全卸载!!!(比如maya,cad,3dsmax等).有时手动删除注册表重装之后还是会出现各种问题,每个版本的C++Runtime和.NET f ...
- maya2013无法安装卸载激活失败
AUTODESK系列软件着实令人头疼,安装失败之后不能完全卸载!!!(比如maya,cad,3dsmax等).有时手动删除注册表重装之后还是会出现各种问题,每个版本的C++Runtime和.NET f ...
- maya2014无法安装卸载激活失败
AUTODESK系列软件着实令人头疼,安装失败之后不能完全卸载!!!(比如maya,cad,3dsmax等).有时手动删除注册表重装之后还是会出现各种问题,每个版本的C++Runtime和.NET f ...
- maya2015无法安装卸载激活失败
AUTODESK系列软件着实令人头疼,安装失败之后不能完全卸载!!!(比如maya,cad,3dsmax等).有时手动删除注册表重装之后还是会出现各种问题,每个版本的C++Runtime和.NET f ...
- maya2017无法安装卸载激活失败
AUTODESK系列软件着实令人头疼,安装失败之后不能完全卸载!!!(比如maya,cad,3dsmax等).有时手动删除注册表重装之后还是会出现各种问题,每个版本的C++Runtime和.NET f ...
- maya2018无法安装卸载激活失败
AUTODESK系列软件着实令人头疼,安装失败之后不能完全卸载!!!(比如maya,cad,3dsmax等).有时手动删除注册表重装之后还是会出现各种问题,每个版本的C++Runtime和.NET f ...
- 02.Windows2012R2安装360安全卫士失败及无法卸载问题
问题: Windows 2012 R2 安装360安全卫士失败及无法卸载,导致网络无法通信问题解决. 解决:1.进入 Windows2012R2 安全模式下:2.进行覆盖安装360安全卫士:3.覆盖安 ...
- Navicat Premium 12.1.16.0安装与激活
声明:本文所提供的所有软件均来自于互联网,仅供个人研究和学习使用,请勿用于商业用途,下载后请于24小时内删除,请支持正版! 本文介绍Navicat Premium 12的安装.激活与基本使用.已于20 ...
- Navicat Premium 12.1.12.0安装与激活
转载自:Navicat Premium 12.1.12.0安装与激活 作者:丿记忆灬永殇丨 链接:https://www.jianshu.com/p/5f693b4c9468 navicat12112 ...
随机推荐
- 百度地图 JS API开发Demo01
百度地图DEMO <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http: ...
- CHSpecialEffect(特效)
1.CALayer 动画 1.1 转场动画CALayer (Transition) 2.UIView效果 毛玻璃CHBlurEffect
- redis-淘汰策略
将redis用作缓存时,如果内存空间用满,就会自动驱逐老的数据.默认情况下,memcached就是这种方式. LRU是Redis唯一支持的回收算法. maxmemory配置指令 maxmemory用于 ...
- 51nod1478(yy)
题目链接: http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1478&judgeId=365133 题意: 中文题诶 ...
- 解决vue-cli相对路径问题 about css assert path ,two Solution(css路径的问题解决方案) #179
https://github.com/vuejs/vue-cli/issues/179
- linux硬盘IO优化相关资料整理
内核相关参数 相关内核参数,有条件的话可以修改参数测试验证一下. 1./proc/sys/vm/dirty_ratio 这个参数则指定了当文件系统缓存脏页数量达到系统内存百分之多少时(如10%),系统 ...
- kuangbin专题十六 KMP&&扩展KMP HDU1238 Substrings
You are given a number of case-sensitive strings of alphabetic characters, find the largest string X ...
- Java技术列表
完整的java技术列表,可以在oracle官网找到: https://www.oracle.com/technetwork/java/javaee/tech/index.html JSR: Java ...
- Jenkins利用官网上的rpm源安装
官网网址:https://pkg.jenkins.io/redhat/ (官网上有安装的命令,参考网址) 安装jdk yum install -y java-1.8.0- ...
- springcloud系列四 搭建服务模块重点讲解
首先这个服务地址:一定不要写错,是自己注册中心开启的地址 如果注意到这些了,可以简单的进行操作,也可以不需要mybatis与数据库连接,在controller里直接返回相应的数据可以了,不用这么幸苦的 ...
