HTML5- Canvas入门（三）

前两章我们掌握了线段、矩形和多边形的绘制方法，今天我们主要是学习如何绘制圆弧和贝塞尔曲线。

圆弧的绘制

圆弧可以理解为一个圆上的某部分线段，在canvas中，绘制一条圆弧的语法如下：

ctx.arc( 圆心x坐标, 圆心y坐标, 圆的半径r , 开始角度, 结束角度 );

其中的 “开始角度” 和 “结束角度” 是相对360度的顺时针的极坐标而言的，可配合下图理解：

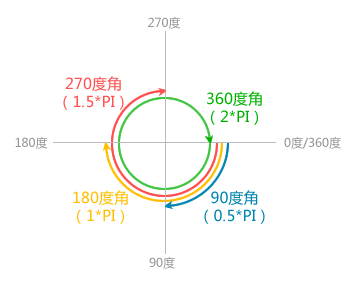
我们来一个例子，绘制一个圆心坐标为(80,80)，半径为40，开始角度为30度，结束角度为90度，那么可以这样绘制：

<canvas id="myCanvas" width="200" height="200" style="border:solid 1px #CCC;">
您的浏览器不支持canvas，建议使用最新版的Chrome
</canvas>

<script>
var c = document.getElementById("myCanvas");
var ctx = c.getContext("2d"); //获取该canvas的2D绘图环境对象
ctx.arc( 80, 80, 40, 1/6*Math.PI, 1/2*Math.PI);
ctx.stroke();  //描边
</script>

其中开始角和结束角我们分别设定为“1/6*Math.PI”和“1/2*Math.PI”，是因为canvas里的角度是以PI（π）为单位的，在js中写作Math.PI，你可以把一个PI理解为180度，那么30度便是1/6个PI。上述代码效果如下：

开始角和结束角也可以是负值，则角度从0度开始以逆时针方式获取：

var c = document.getElementById("myCanvas");
var ctx = c.getContext("2d"); //获取该canvas的2D绘图环境对象
ctx.arc( 80, 80, 40, -1/6*Math.PI, -1/2*Math.PI);
ctx.stroke();  //描边

我们可以很轻松地来绘制一个完整的圆，将起始角设为0度，结束角设为360度（2*Math.PI）即可：

var c = document.getElementById("myCanvas");
var ctx = c.getContext("2d"); //获取该canvas的2D绘图环境对象
ctx.arc( 80, 80, 40, 0, 2*Math.PI);

ctx.lineWidth = 3;  //描边宽度为3px
ctx.strokeStyle = "yellow";
ctx.stroke();  //描边
ctx.fillStyle = "#4DA6FF";
ctx.fill(); //填充颜色

注意给圆填充颜色我们使用的是 .fill() 方法，和多边形的填充方式一样。

接着说说 arc() 的好兄弟 arcTo() 方法，它可以在两条线段之间连接起一条弧线，其语法如下

ctx.arcTo( 起点切线末端x坐标, 起点切线末端y坐标, 终点x坐标, 终点y坐标, 圆的半径r );

可以配合下图理解：

我们先不管什么“连接两条线段”的事情，单纯看下arcTo()绘制了怎样的一条圆弧：

<canvas id="myCanvas" width="200" height="200" style="border:solid 1px #CCC;">
您的浏览器不支持canvas，建议使用最新版的Chrome
</canvas>

<script>
var c = document.getElementById("myCanvas");
var ctx = c.getContext("2d"); //获取该canvas的2D绘图环境对象
ctx.moveTo(20,20);           // 创建开始点
ctx.arcTo(60,20,60,60,40); // 创建圆弧路径
ctx.stroke();
</script>

效果如下：

那么我们利用arcTo()方法来连接两条直线吧：

<canvas id="myCanvas" width="200" height="200" style="border:solid 1px #CCC;">
您的浏览器不支持canvas，建议使用最新版的Chrome
</canvas>

<script>
var c = document.getElementById("myCanvas");
var ctx = c.getContext("2d"); //获取该canvas的2D绘图环境对象
ctx.moveTo(20,20);
ctx.lineTo(60,20);
ctx.arcTo(100,20,100,60,40); // 创建圆弧路径
ctx.lineTo(100,100);
ctx.stroke();
</script>

效果如下：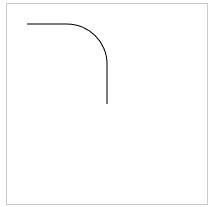

需要知道的是 arc() 不会影响画笔的位置，而 arcTo() 会把画笔移到圆弧线的终点位置。

曲线的绘制

无论是arc()抑或arcTo()，均是绘制了一个正圆上的部分圆弧线段，下面讲讲更灵活的曲线的绘制。

首先介绍的是canvas中贝塞尔曲线的绘制。使用过AI等专业矢量制图软件的朋友相信能很好地理解这一部分。我们先看下在制图软件中用钢笔工具绘制一条贝塞尔曲线的过程：

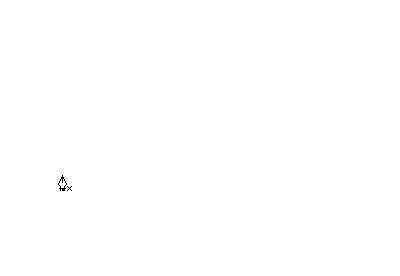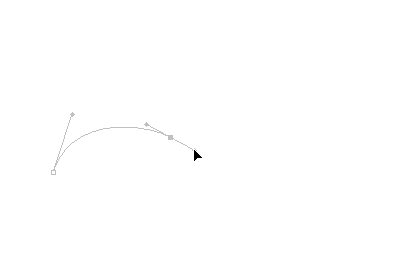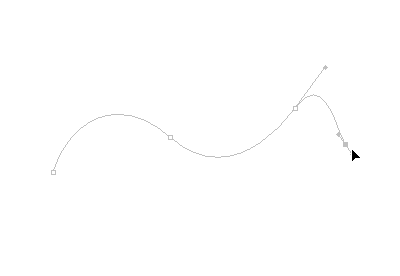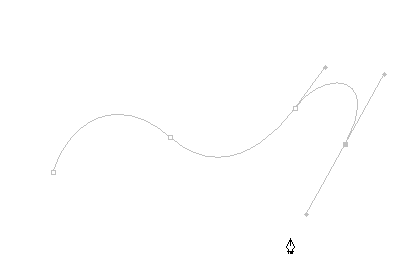
可以看到每两点可以连成一条贝塞尔路径，且每一个点都有一条方位控制线来控制曲线的弯曲程度和走向，在canvas中也是以类似形式控制贝塞尔曲线的形状。

我们先来看看bezierCurveTo()的实现方式，它称作“三次方贝塞尔曲线”，其语法为：

ctx.bezierCurveTo( CSx, CSy, CEx, CEy, Ex, Ey );

其中CSx、CSy表示贝塞尔曲线起点方向控制线末端的x坐标和y坐标。CEx、CEy表示贝塞尔曲线终点方向控制线末端的x坐标和y坐标。Ex、Ey表示贝塞尔曲线终点坐标。

参考图如下，图中的贝塞尔曲线起点坐标为（20,20），终点坐标为（200,20），起点的方向控制线末端坐标为（20,100），终点的方向控制线末端坐标为（200,100）：

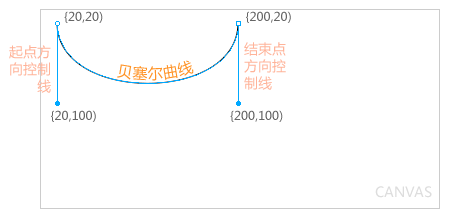
有的朋友可能会问为何bezierCurveTo()方法没有起始点的参数，答案是起始点默认为bezierCurveTo()方法执行之前画笔所在的位置，我们可以通过ctx.moveTo(x,y)来确定起始点的位置。

如上图所示的贝塞尔曲线我们可以这样绘制：

<canvas id="myCanvas" width="300" height="150" style="border:solid 1px #CCC;">
您的浏览器不支持canvas，建议使用最新版的Chrome
</canvas>

<script>
var c = document.getElementById("myCanvas");
var ctx = c.getContext("2d"); //获取该canvas的2D绘图环境对象
ctx.moveTo(20,20);   //确定起始点
ctx.bezierCurveTo( 20, 100, 200, 100, 200, 20 );
ctx.stroke();  //描边
</script>

我们可以绘制两条或者多条连在一起的贝塞尔曲线，从而塑造我们想要的曲线：

<canvas id="myCanvas" width="400" height="250" style="border:solid 1px #CCC;">
您的浏览器不支持canvas，建议使用最新版的Chrome
</canvas>

<script>
var c = document.getElementById("myCanvas");
var ctx = c.getContext("2d"); //获取该canvas的2D绘图环境对象
ctx.moveTo(20,120);   //确定起始点
ctx.bezierCurveTo( 20, 200, 200, 200, 200, 120 );   //绘制第一条贝塞尔曲线
ctx.bezierCurveTo( 200, 20, 380, 20, 380, 120 );  //绘制第二条贝塞尔曲线，该曲线起点为上一条曲线终点（200，120）
ctx.stroke();  //描边
</script>

效果如下：

使用过矢量制图软件的朋友可能有个地方会困惑，那就是我们很多时候开始绘制一条曲线时（起点不做拉伸），该曲线的起点是没有任何方向控制线的，如下图：

如果我们要绘制一条起点不做方向控制的曲线，那么bezierCurveTo()方法就不再适用了。

针对这种情况，可以通过 quadraticCurveTo() 方法来解决，它称作“二次方贝塞尔曲线”，语法为

ctx.quadraticCurveTo( CEx, CEy, Ex, Ey );

其中CEx、CEy表示曲线终点方向控制线末端的x坐标和y坐标。Ex、Ey表示曲线终点坐标。至于曲线起点则跟bezierCurveTo()一样，为该方法执行前画笔所在的位置。

我们试着来绘制一条这样的曲线，它是我在AI中用钢笔工具绘制出来的：

它的矢量轮廓是这样的：

由于起点是没有方向控制线的，我们很容易知道得先绘制一条quadraticCurve，然后再紧接着绘制一条bezierCurve来完成这条曲线。

我们先确定下各点的坐标：

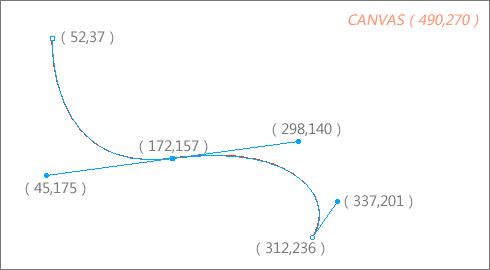
然后轻松写出代码：

<canvas id="myCanvas" width="490" height="270" style="border:solid 1px #CCC;">
您的浏览器不支持canvas，建议使用最新版的Chrome
</canvas>

<script>
var c = document.getElementById("myCanvas");
var ctx = c.getContext("2d"); //获取该canvas的2D绘图环境对象
ctx.moveTo(52,37);   //确定起始点
ctx.quadraticCurveTo( 45, 175, 172, 157 );   //绘制第一条曲线
ctx.bezierCurveTo( 298, 140, 337, 201, 312, 236 );  //绘制第二条曲线
ctx.stroke();  //描边
</script>

效果如下，杠杠的：

本章暂时写到这里，建议有兴趣的朋友多实践，其中贝塞尔曲线部分的知识点可以通过AI等矢量设计软件来加深理解。共勉~