bzoj 3111 蚂蚁 动态规划

题目描述

在一个 n*m 的棋盘上，每个格子有一个权值，初始时，在某个格子的顶点处一只面朝北的蚂蚁，我们只知道它的行走路线是如何转弯，却不知道每次转弯前走了多长。

蚂蚁转弯是有一定特点的，即它的转弯序列一定是如下的形式：右转，右转，左转，左转，右转，右转…左转，左转，右转，右转，右转。即两次右转和两次左转交替出现的形式，最后两次右转（最后两次一定是右转）后再多加一次右转。我们还知道，蚂蚁不会在同一个位置连续旋转两次，并且蚂蚁行走的路径除了起点以外，不会到达同一个点多次，它最后一定是回到起点然后结束自己的行程，而且蚂蚁只会在棋盘格子的顶点处转弯。

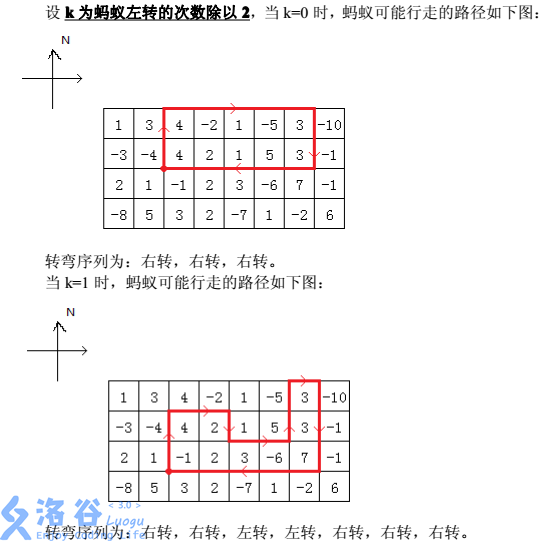
现在已知棋盘大小、每个格子的权值以及左转次数/2 的值，问蚂蚁走出的路径围出的封闭图形，权值之和最大可能是多少。

输入输出格式

输入格式：

在输入文件ant.in 中，第一行三个数n,m,k。意义如题目描述。

接下来一个n 行m 列的整数矩阵，表示棋盘。

输出格式：

一个数，表示蚂蚁所走路径围出的图形可能的最大权值和。

输入输出样例

输入样例#1： 复制

2 5 2
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1

输出样例#1： 复制

-8

说明

【样例说明】

除了第一行的第二个和第一行的第四个都要围起来才至少合法。

【数据规模与约定】

10%的数据所有格子中权值均非负

另20%的数据n=2

另30%的数据k=0

100%的数据1≤n≤100,1≤m≤100,0≤k≤10 保证存在合法路径，数据有梯度，格子中每个元素的值绝对值不超过 10000

P3335 这个题思维难度还是有的。。(至少我是这么想的。。大佬就别吐槽我了)

首先，通过题目描述，我们可以在纸上画一画，可以发现，图像一定是像长城一样的

就是好多个矩形它们的底在一条直线上，高和宽不同，而且，还有一点就是它是高低相间的

而且由右转形成高峰，由左转形成低谷。

那么我们可以枚举图的右下角(i,j)，那么有两种情况：

一:第j-1列和第j列在同一个矩形里；

二:第j-1列和第j列在不同的矩形里；

我们要记录的状态与点(i,j),p(指的是当前枚举的是第p个矩形),h(当前枚举的举行高度为i-h+1)有关

所以用f[i][j][p][h]来记录‘一’情况的状态，用g[i][j][p][h][0/1]来记录‘二’情况的状态

这里0表示上一个矩形高度高于h，1表示低于h；

那么转移就好写了：

f[i][j][p][h]=max(f[i][j-1][p][h],g[i][j-1][p-1][h][p%2])+s[i][j]-s[h-1][j];

对了，这里这个s数组求的是每一列的前缀和，可以在输入中预处理出来，方便计算用；

关于g数组的维护，我们已经维护出f数组的第j列了

那么这一列所在的矩形要么是低谷，要么是高峰，我们都要考虑

->高峰：

g[i][j][p][h][0]=max(f[i][j][p][h-1],g[i][j][p][h-1][0]);

->低谷：

g[i][j][p][h][1]=max(f[i][j][p][h+1],g[i][j][p][h+1][1]);

当然我们可以在计算过程中更新答案，还可以省掉i这一维

因为从方程中就可以看出来i其实没有参与转移

 #pragma GCC optimize(2)
 #pragma G++ optimize(2)
 #pragma GCC target ("avx")
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 const int maxn=;
 const int Inf=;
 int n,m,k,ans;
 int a[maxn][maxn];
 int f[maxn][][maxn];
 int g[maxn][][maxn][];
 int s[maxn][maxn];
 void ini()
 {
     scanf("%d%d%d",&n,&m,&k);
     //因为有2*k次左转，所以总矩形数就是k*2+1
     k=k*+;
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=m;j++)
         {
             scanf("%d",&a[i][j]);
             s[i][j]=s[i-][j]+a[i][j];
         }
     }
     //预处理 因为要求最大值，所以边界赋值为-Inf；
     for(int p=;p<=k;p++)
     {
         for(int h=;h<=n;h++)
         {
             f[][p][h]=-Inf;
             g[][p][h][]=-Inf;
             g[][p][h][]=-Inf;
         }
     }
 }
 void dp()
 {
     ans=-Inf;
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=m;j++)
         {
             for(int p=;p<=k;p++)
             {
                 for(int h=i;h>=;h--)//维护f数组
                 {
                     f[j][p][h]=max(f[j-][p][h],g[j-][p-][h][p%])+s[i][j]-s[h-][j];
                 }
                 //维护g数组
                 g[j][p][][]=-Inf;
                 //0指当前矩形比下一个高，所以从高到低更新，才可以确保取最大值的矩形一定是高的
                 for(int h=;h<=i;h++)
                 {
                     g[j][p][h][]=max(f[j][p][h-],g[j][p][h-][]);
                 }
                 g[j][p][i][]=-Inf;
                 //1指当前矩形比下一个底，所以从低到高更新，才可以确保取最大值的矩形一定是低的
                 for(int h=i-;h>=;h--)
                 {
                     g[j][p][h][]=max(f[j][p][h+],g[j][p][h+][]);
                 }
             }
             //更新答案，因为最后一列一定是高的，所以用0转移；
             ans=max(ans,max(f[j][k][i],g[j][k][i][]));
         }
     }
 }
 int main()
 {
     ini();//读入一些数据
     dp();
     printf("%d\n",ans);
     return ;
 }