KMP字符串匹配算法翔解❤

看了Angel_Kitty学姐的博客，我豁然开朗，写下此文：

那么首先我们知道，kmp算法是一种字符串匹配算法，那么我们来看一个例子。

比方说，现在我有两段像这样子的字符串：

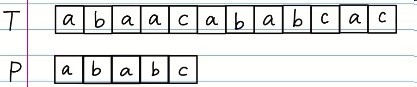
分别是T和P，很明显，P比T的长度要短很多，我们要做的事情呢，就是找找T中有没有和P相同的一段。

如果按照最简单的办法来做匹配的话，我们一般是一个一个字母的来做。

像这样：

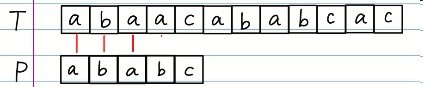
很显然，图中前面3位都是能匹配的，而第四位却不能匹配，怎么办？

这样：

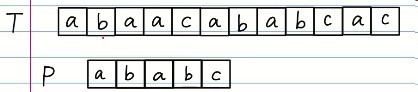
我们就会将整个P字符串向右移动一格，又重新开始，从T中b处与P中第一个a处开始匹配。

如此往复，显然这样是很慢的，因为我们来考虑考虑这样一种极端的情况：

像这样，显然一位一位匹配是会做许多重复的操作的。

那么现在我们来考虑使用一下kmp算法。

怎么做呢？

首先我们需要处理一个叫做前缀表(prefix table)的东西（有些博客说是next[]数组，其实是一样的）。

什么是前缀呢？比如说，P字符串为a b a b c，那么P的前缀即为a，a b，a b a，a b a b和a b a b c共五个。

所以，做kmp算法时，我们先要把我们要搜索的那一个字符串的所有前缀都写出来。这是第一步。

好，那么第二步，我们就要将之前处理出的所有前缀当做不同的几个字符串。

然后，我们对每个这样的前缀字符串处理一下，处理出一个叫做最长公共前后缀的东西。

最长公共前后缀是比原来字符串要短的前缀与后缀最长公共部分的长度，这是什么意思呢？听起来特别拗口。

比方说，我们来看看第四个前缀字符串。很显然，它的最长前缀是a b a，最长后缀是b a b(忽略本身)。

明显这两者是不同的，所以长度取3时是不行的。那么我们取2，此时前缀是a b，后缀是a b，二者相等。

这时我们就将2称作字符串a b a b的最长公共前后缀。

如图，我们处理出了前缀表中的所有最长公共前后缀。

而在KMP算法中，前缀表里长度等于本身的那个并不需要处理，舍去，而需要在最上面添加一个-1。

（等下模拟时，其作用就显而易见了）。

现在我们已经处理好了prefix table，即-1 0 0 1 2 0。

接下来，进行第三步，将prefix table与P字符串对应，并标好下标index

1、          2、

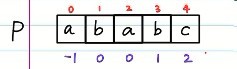
如图，上层是index，下层是prefix。

然后，我们模拟一下KMP算法是如何利用处理好的前缀表来计算运行的。

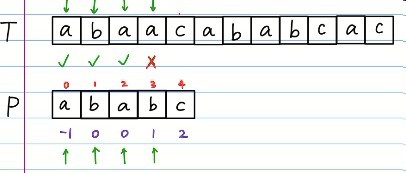
如图，前面3位，我们还是如之前一样完美匹配，但是到了第四位，就匹配不了了，怎么办呢？

不同以往，我们不再是往右移一格，而是跳到这一位对应的prefix所指的index处，!@#$%^&*...好绕啊啊啊！

上图吧：

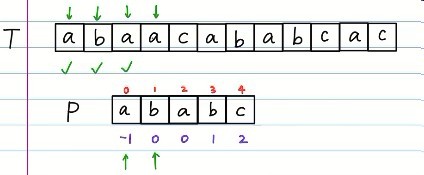
此时待匹配的位置的index，是不是就是之前发生错误的那个第四位所对应的prefix呢？

这样，我们便可以直接从P中第二位开始重新匹配啦！！！

p.s.忘了说了，如果prefix是-1，那么就直接向右移一格。

真是神奇讷、

不知道读者是否还记得之前提出的极端情况。

如果用KMP算法，处理好前缀表后，是不是这样：

所以 当匹配到a b时，那么就直接会跳到index为3的a处，而跳过匹配前面3个a，时间复杂度大大降低↓↓↓。

至于代码：

想看代码可以直接看我的随笔《从2017暑假到现在手打的模板》之二十三。