MATLAB卷积运算（conv、conv2）解释

来源：https://www.cnblogs.com/hyb221512/p/9276621.html

1.conv（向量卷积运算）

所谓两个向量卷积，说白了就是多项式乘法。
比如:p=[1 2 3],q=[1 1]是两个向量，p和q的卷积如下：
把p的元素作为一个多项式的系数，多项式按升幂（或降幂）排列，比如就按升幂吧，写出对应的多项式：1+2x+3x^2;同样的，把q的元素也作为多项式的系数按升幂排列，写出对应的多项式：1+x。

卷积就是“两个多项式相乘取系数”。
（1+2x+3x^2）×（1+x）=1+3x+5x^2+3x^3
所以p和q卷积的结果就是[1 3 5 3]。

记住，当确定是用升幂或是降幂排列后，下面也都要按这个方式排列，否则结果是不对的。
你也可以用matlab试试
p=[1 2 3]
q=[1 1]
conv(p,q)
看看和计算的结果是否相同。

>> p=[1 2 3];
q=[1 1];
conv(p,q)

ans =

1 3 5 3

2.conv2（二维矩阵卷积运算）

语法：
conv2(原图像,卷积核)

a=[1 1 1;1 1 1;1 1 1];
b=[1 1 1;1 1 1;1 1 1];
>> conv2(a,b)

ans =

1     2     3     2     1
     2     4     6     4     2
     3     6     9     6     3
     2     4     6     4     2
     1     2     3     2     1

>> conv2(a,b,'valid')

ans =

9

'valid'就意味着不对原图像padding.

>> conv2(a,b,'same')

ans =

4     6     4
     6     9     6
     4     6     4

same的解释：

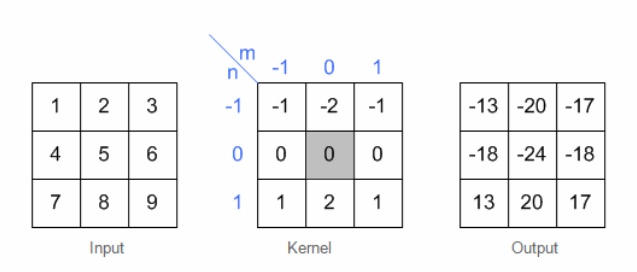
卷积的时候需要对卷积核进行180的旋转，同时卷积核中心与需计算的图像像素对齐，输出结构为中心对齐像素的一个新的像素值

>> conv2(a,b,'full')

ans =

1     2     3     2     1
     2     4     6     4     2
     3     6     9     6     3
     2     4     6     4     2
     1     2     3     2     1

图中蓝色为原图像，白色为对应卷积所增加的padding，通常全部为0，绿色是卷积后图片。图的卷积的滑动是从卷积核右下角与图片左上角重叠开始进行卷积，滑动步长为1，卷积核的中心元素对应卷积后图像的像素点。