【ZROJ2730】简单题 可持久化分块题解

Description

给定一棵 \(n\) 个节点的树，每次询问编号为 \([l, r]\) 的点中有多少个是祖先关系。

\(n, q \le 10^5\)。

Solution

直接做的话树上的祖先关系不好统计，那么转化到 \(\texttt{dfs}\) 序上，如果 \(u\) 是 \(v\) 的祖先那么 \(dfn_u \le dfn_v < dfn_u + siz_u\)。

把 \([dfn_u, dfn_u + siz_u - 1]\) 看成一条线段，把树上的点拆成一条线段和一个点，那么问题就变成了用 \([l, r]\) 的线段覆盖 \([l, r]\) 的点，能够覆盖多少次。

首先对点分块，\(f_{i, j}\) 表示前 \(i\) 条线段在第 \(j\) 个块中能覆盖多少次，可以对每一个块中的点做一遍前缀和，加入一条线段就在对应的块中查询。

接下来考虑散点怎么处理，每次我们要处理一个散点在编号为 \([l, r]\) 的线段中被覆盖的次数，现在对于线段建主席树，把 \([l, r]\) 拆成主席树上的两个点，相减计算贡献。

那么在主席树上要做 \(O(n \sqrt n)\) 次操作，时间复杂度 \(O(n \sqrt n \log n)\)，然后调整块长可以做到 \(O(n \sqrt{n \log n})\)，这是官方题解做法。

现在开始优化主席树部分，我们发现修改有只有 \(n\) 次，而查询有 \(n \sqrt n\) 次，使用主席树做修改是非常浪费的，考虑用可持久化值域分块平衡两部分复杂度。

分块本质上也可以看作一个树形结构，由于要可持久化，所以把分块树建出来，每一个块用一个关键点表示，每一个散点用一个叶子表示。

那么每次修改只会影响 \(O(\sqrt n)\) 个关键点，以及散块的 \(O(\sqrt n)\) 个叶子，对于散块我们暴力复制所有点重构一遍，所有代表整块的关键点我们也复制一份，但是只在这些点上打标记，不递归到它下面的叶子。

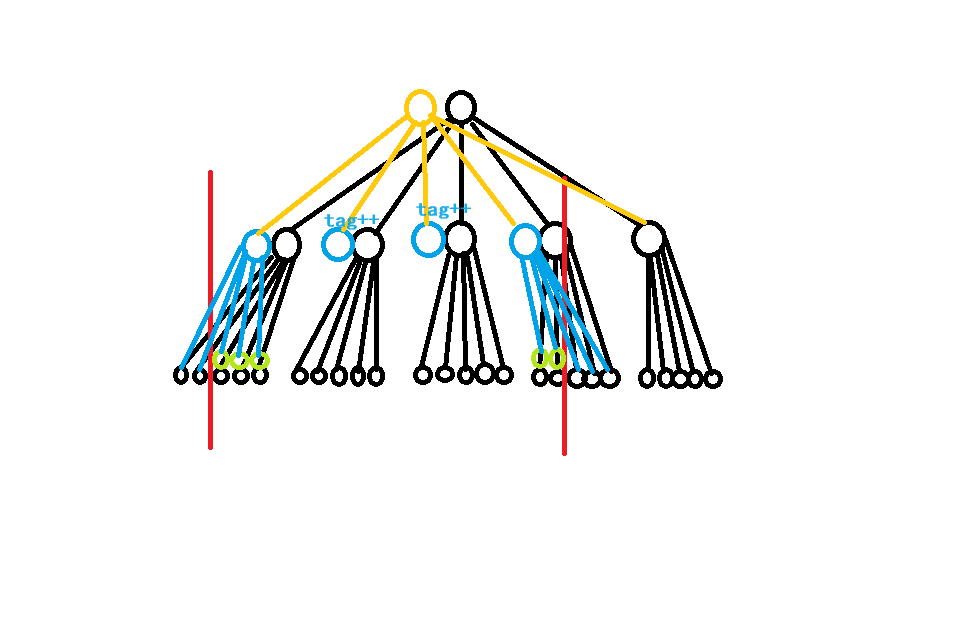
容易发现单词修改只会影响 \(O(\sqrt n)\) 个点，从而时空复杂度为 \(O(n \sqrt n)\)。

Code

点击查看代码

#include <iostream>
#include <vector>
#pragma GCC optimize("Ofast")

using namespace std;
using LL = long long;

const int N = 1e5 + 5;
const int kL = 233, M = N / kL + 2;
const int tL = N * kL; 

int n, q, now;
int fa[N], dfn[N], siz[N], rt[N];
int bl[N], cnt;
int L[M], R[M], f[N][M], c[M][N];
vector<int> e[N];

void dfs (int u) {
  dfn[u] = ++now;
  siz[u] = 1;
  for (auto v : e[u]) {
    if (v != fa[u]) {
      dfs(v);
      siz[u] += siz[v];
    }
  }
}

struct Sqrt_tree {
  int totr, tots, totl, toti;
  int son[N][M + 2];
  int lson[N * 3][kL + 2];
  int val[tL * 2], tag[tL], id[tL]; 

  void builds (int &k, int l, int r) {
    k = ++tots, id[k] = ++toti;
    for (int i = l; i <= r; ++i) {
      lson[id[k]][i - l + 1] = ++totl;
    }
  }

  void build (int &k) {
    k = ++totr;
    for (int i = 1; i <= cnt; ++i) {
      builds(son[k][i], L[i], R[i]);
    }
  }

  void adds (int t, int &k, int l, int r, int L, int R) {
    id[k = ++tots] = ++toti, tag[k] = tag[t];
    copy(lson[id[t]] + 1, lson[id[t]] + R - L + 2, lson[id[k]] + 1);
    for (int i = l; i <= r; ++i) {
      int p = ++totl;
      val[p] = val[lson[id[t]][i - L + 1]] + 1;
      lson[id[k]][i - L + 1] = p;
    }
  }

  void addall (int t, int &k) {
    id[k = ++tots] = id[t], tag[k] = tag[t] + 1;
  } 

  void add (int t, int &k, int l, int r) {
    k = ++totr;
    int bl = ::bl[l], br = ::bl[r];
    copy(son[t] + 1, son[t] + cnt + 1, son[k] + 1);
    if (bl == br) {
      adds(son[t][bl], son[k][bl], l, r, L[bl], R[bl]);
    }
    else {
      adds(son[t][bl], son[k][bl], l, R[bl], L[bl], R[bl]);
      adds(son[t][br], son[k][br], L[br], r, L[br], R[br]);
      for (int i = bl + 1; i < br; ++i) {
        addall(son[t][i], son[k][i]);
      }
    }
  }

  int count (int k, int x) {
    int s = son[k][bl[x]];
    return val[lson[id[s]][x - L[bl[x]] + 1]] + tag[s];
  }
} t;

LL query (int x, int l, int r) {
  int bl = ::bl[l], br = ::bl[r];
  auto qry = [&](int i) -> int {
    return t.count(rt[x], dfn[i]);
  };
  LL res = 0;
  if (bl == br) {
    for (int i = l; i <= r; ++i) {
      res += qry(i);
    }
  }
  else {
    for (int i = l; i <= R[bl]; ++i) {
      res += qry(i);
    }
    for (int i = bl + 1; i < br; ++i) {
      res += f[x][i];
    }
    for (int i = L[br]; i <= r; ++i) {
      res += qry(i);
    }
  }
  return res;
}

int main () {
  ios::sync_with_stdio(0);
  cin.tie(0); cout.tie(0);
  cin >> n;
  for (int i = 2; i <= n; ++i) {
    cin >> fa[i];
    e[fa[i]].push_back(i);
  }
  dfs(1);
  for (int i = 1; i <= n; ++i) {
    bl[i] = (i - 1) / kL + 1;
  }
  cnt = bl[n];
  for (int i = 1; i <= cnt; ++i) {
    L[i] = R[i - 1] + 1;
    R[i] = min(L[i] + kL - 1, n);
  }
  for (int i = 1; i <= cnt; ++i) {
    for (int j = L[i]; j <= R[i]; ++j) {
      ++c[i][dfn[j]];
    }
    for (int j = 1; j <= n; ++j) {
      c[i][j] += c[i][j - 1];
    }
  }
  for (int i = 1; i <= n; ++i) {
    for (int j = 1; j <= cnt; ++j) {
      f[i][j] = f[i - 1][j] + c[j][dfn[i] + siz[i] - 1] - c[j][dfn[i] - 1];
    }
  }
  t.build(rt[0]);
  for (int i = 1; i <= n; ++i) {
    t.add(rt[i - 1], rt[i], dfn[i], dfn[i] + siz[i] - 1);
  }
  cin >> q;
  for (LL la = 0, l, r; q--; ) {
    cin >> l >> r;
    l ^= la, r ^= la;
    l = l % n + 1, r = r % n + 1;
    if (l > r) swap(l, r);
    cout << (la = (query(r, l, r) - query(l - 1, l, r))) << '\n';
  }
  return 0;
}