NOIP模拟测试A2

好像是去年 8 月 1 日的模拟赛，主题采自南昌起义。

背景

A. 南

一道可爱的期望 DP。

一般来说，期望 DP 都是逆推，从最终状态往前推，这题也不例外。

这道题难度主要在于，第 $k$ 次购买的价格为 $k$，即价格与购买次数有关。

那我们就不能直接进行转移了，而是需要根据期望次数进行转移。

所以我们定义 $f[i]$ 为已经获得 $i$ 种武器，想要获得 $n$ 种武器的期望次数。

初始状态 $f[n] = 0$，即已经获得 $n$ 种武器后想要取完 $n$ 种武器的期望次数为 $0$。

$f[i]$ 的转移还是很容易能想到的，分两种情况处理。

买到了已经有的类型，得到 $f[i] = f[i] + 1$，已经获得的武器种类数保持不变，仍然为 $i$。
买到之前没有的类型，得到 $f[i] = f[i+1]+1$，拥有的武器种类数增加了 $1$。

于是我们得到式子：

\[f[i] = \frac{i}{n} \times (f[i] + 1) + \frac{n-i}{n}\times (f[i + 1]+1)
\]

这个式子可以化简

\[f[i] = f[i + 1] + \frac{n}{n-i}
\]

定义 $g[i]$ 为已经获得 $i$ 种武器，想要获得 $n$ 种武器的期望钱数。

同理，初始状态为 $g[i] = 0$，仍然分取到已经有的和取到没有的两种情况处理。

\[g[i] = \frac{i}{n}\times(g[i] + f[i] + 1) + \frac{n-i}{n}\times(g[i + 1]+f[i+1]+1)
\]

每次加的钱数都是在上一次的基础上加了 $1$，无论是买到已获得的还是未获得的。

这个式子仍然可以化简：

\[g[i] = \frac{i}{n-i}\times f[i] + g[i + 1]+f[i + 1]+\frac{n}{n-i}
\]

Code：

for(int i = n - 1;i >= 0; i--)

		f[i] = f[i + 1] + (double)n / (double)(n - i);

	for(int i = n - 1;i >= 0; i--)

		g[i] = (double)i / (double)(n - i) * f[i] + g[i + 1] + f[i + 1] + (double)n / (double)(n - i);

B. 昌

要求根结点的最大值。

我们先假设根结点的最大值大于等于 $x$，那么对于 $\text{min}$ 操作来说，儿子的权值必须都大于等于 $x$；对于 $\text{max}$ 操作来说，儿子的权值至少要有一个大于等于 $x$。

依次类推，我们就可以找到这棵树有多少叶子结点的权值需要大于等于 $x$，设这个值为 $cnt$，那么 $x$ 的最大值就是 $k - cnt + 1$，$k$ 为叶子个数。

所以我们可以求出来 $cnt$，用它来求 $x$。

设 $f[u]$ 为以 $u$ 为根的子树内，至少有 $f[u]$ 个叶子结点需要大于某个值。

对于叶子结点，有 $f[u] = 1$。

对于 $\text{max}$ 操作：$f[u] = \text{min}_{v \in son[u]}f[v]$

对于 $\text{min}$ 操作：$f[u] = \Sigma_{v \in son[u]} f[v]$

（对应的就是最开始那几句）

最终答案为 $k - f[1] + 1$。

Code：

void dfs(int x) {

	if(e[x].empty()) {

		dp[x] = 1;

		return;

	}

	if(a[x] == 1) {

		dp[x] = INT_MAX >> 1;

		for(int i : e[x]) {

			dfs(i);

			dp[x] = min(dp[x],dp[i]);

		}

	} else {

		dp[x] = 0;

		for(int i : e[x]) {

			dfs(i);

			dp[x] += dp[i];

		}

	}

}

C. 起

不想写了，挂个官方题解

D. 义

好像是根号分治。

一个没听说过的东西，考后查了查，是一种思想，将要处理的整体分为前 $\sqrt{n}$ 和剩余部分分别处理。

在这道题里十分的明显。

对于前 $\sqrt{n}$ 种物品，每一种物品都有取完的可能。

但对于 $\sqrt{n} + 1$ 到 $n$ 种物品，如果把物品取完，就会超过背包容量，所以物品都取不完，相当于物品数量是无穷的。

所以我们可以分开进行 DP。

对于前 $\sqrt{n}$ 种物品，定义 $f[i][j]$ 为取完第 $i$ 种物品，背包容量已经用 $j$。

有

\[f[i][j] = f[i-1][j] + f[i][j-i]-f[i-1][j-i \times (i +1)]
\]

假设有一条线段，表示我们背包的容量。

$f[i-1][j]$ 表示不拿 $i$ 物品，$f[i][j-i]$ 表示再拿一个 $i$ 物品，要减去多拿的方案数。

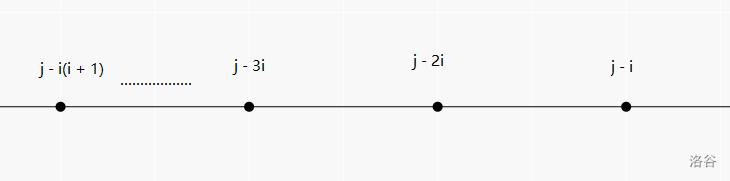
对于 $f[i][j]$，是由 $f[i][j - i]$ 转移而来的，$f[i][j - i]$ 是由 $f[i][j - 2i]$ 转移而来，但显然，不能拿 $i(i+1)$ 个或以上，所以需要减去这部分。

再考虑剩下的部分，定义 $g[i][j]$ 表示拿了 $i$ 件 $\sqrt{n} + 1$ 到 $n$ 的物品，使用背包容量为 $j$，有

\[g[i][j + i] = g[i][j+i]+g[i][j]
\]

表示每个物品都增加 $1$ 的容量，变成下一种物品，就是不拿第 $\sqrt{n} + 1$ 种物品

\[g[i][j + \sqrt{n} +1] = g[i][j + \sqrt{n} +1] + g[i][j]
\]

表示拿一个第 $\sqrt{n} +1$ 种物品。

最后把两个数组的方案数相乘相加。

Code：

    m = sqrt(n);

    f[0][0] = f[1][0] = 1;

    int k = 0;

    for (int i = 1; i <= m; i++) {

        k ^= 1;

        for (int j = 1; j <= n; j++) {

            f[k][j] = f[k ^ 1][j];

            if (j >= i)

                f[k][j] = (f[k][j] + f[k][j - i]) % MOD;

            if (j >= i * (i + 1))

                f[k][j] = (f[k][j] - f[k ^ 1][j - i * (i + 1)] + MOD) % MOD;

        }

    }

    g[0][0] = 1;

    for (int i = 0; i <= m; i++)

        for (int j = 0; j <= n; j++) {

            if (j + i <= n && i)

                g[i][j + i] = (g[i][j + i] + g[i][j]) % MOD;

            if (j + m + 1 <= n)

                g[i + 1][j + m + 1] = (g[i + 1][j + m + 1] + g[i][j]) % MOD;

        }

    g[1][0] = 1;

    for (int i = 0; i <= n; i++)

        for (int j = 1; j <= m; j++)

            ans = (ans + 1ll * f[k][i] * g[j][n - i] % MOD) % MOD;