LeetCode 332. Reconstruct Itinerary 最小欧拉路径

题意

给N个单词表示N个点，和N-1个单词对，表示可以走的路径，求字典序最小的总路径。

首先说下这么暴力DFS能过。暴力的我都不敢写= =

class Solution {
public:
    vector<string> findItinerary(vector<vector<string> >& tickets) {
        map<string, vector<string> > mp;

        for (int i = 0; i < tickets.size(); i++) {
            string from = tickets[i][0];
            string to = tickets[i][1];
            if (mp.find(from) == mp.end()) {
                vector<string> v;
                v.push_back(to);
                mp[from] = v;
            } else {
                mp[from].push_back(to);
            }
        }
        for (map<string, vector<string> >::iterator iter = mp.begin(); iter != mp.end(); iter++) {
            sort(iter->second.begin(), iter->second.end());
        }
        vector<string> res;
        string cur = "JFK";
        res.push_back(cur);
        dfs(cur, mp, res, tickets.size());
        return res;
    }

    bool dfs(string cur, map<string, vector<string> > &mp, vector<string> &res, int n) {
        if (res.size() == n + 1) return true;
        if (mp.find(cur) == mp.end()) return false;
        if (mp[cur].size() == 0) return false;
        for (int i = 0; i < mp[cur].size(); i++) {
            string nxt = mp[cur][i];
            res.push_back(nxt);
            mp[cur].erase(mp[cur].begin() + i);
            if (dfs(nxt, mp, res, n)) return true;
            mp[cur].insert(mp[cur].begin() + i, nxt);
            res.pop_back();
        }
        return false;
    }
};

然后说正解。

如果把每一个字符串当做一个点，每一个字符串对就是一条有向边。那么这么题目就是要求输出最小字典序的欧拉路径。

以下参考 https://www.cnblogs.com/TEoS/p/11376707.html

什么是欧拉路径？欧拉路径就是一条能够不重不漏地经过图上的每一条边的路径，即小学奥数中的一笔画问题。而若这条路径的起点和终点相同，则将这条路径称为欧拉回路。

如何判断一个图是否有欧拉路径呢？显然，与一笔画问题相同，一个图有欧拉路径需要以下几个条件：

• 首先，这是一个连通图
• 若是无向图，则这个图的度数为奇数的点的个数必须是0或2；若是有向图，则要么所有点的入度和出度相等，要么有且只有两个点的入度分别比出度大1和少1

上面这两个条件很好证明。查找欧拉路径前，必须先保证该图满足以上两个条件，否则直接判误即可。

查找欧拉路径的算法有Fluery算法和Hierholzer算法。下面介绍一下Hierholzer算法。

算法流程：

1. 对于无向图，判断度数为奇数的点的个数，若为0，则设任意一点为起点，若为2，则从这2个点中任取一个作为起点；对于有向图，判断入度和出度不同的点的个数，若为0，则设任意一点为起点，若为2，则设入度比出度小1的点为起点，另一点为终点。具体起点的选择要视题目要求而定。
2. 从起点开始进行递归：对于当前节点x，扫描与x相连的所有边，当扫描到一条(x,y)时，删除该边，并递归y。扫描完所有边后，将x加入答案队列。
3. 倒序输出答案队列。（因为这里是倒序输出，我们可以用栈来存储答案，当然用双端队列也可以）

我画图理解一下这个算法，一个欧拉路径其实都是这个样子的

就是从起点到终点的路径上画几个圈。

举两个具体的例子

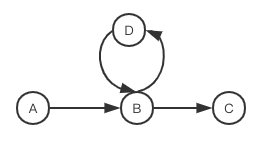
path = []

A --> B --> C 因为C没有再相连的边 所以把C加入路径 path=[C]

　　　　--> D --> B 因为B没有再相连的边 所以把B加入路径 path=[C, B]

　　　　　　D  path=[C, B, D]

　　　B path=[C, B, D, B]

A path=[C, B, D, B, A]

path = []

A --> B --> C --> B --> D 因为D没有再相连的边 所以把D加入路径 path=[D]

　　　　　　　　　 B path=[D, B]

　　　　　　C path=[D, B, C]

　　　B path=[D, B, C, B]

A path=[D, B, C, B, A]

所以无论先遍历的那一条边都能得出正确的欧拉路径，既然题目要求字典序，那么每次选择最小字符串先处理即可。

代码

class Solution {
public:
    vector<string> findItinerary(vector<vector<string> >& tickets) {
        map<string, priority_queue<string,vector<string>,greater<string> > > mp;

        for (int i = 0; i < tickets.size(); i++) {
            string from = tickets[i][0];
            string to = tickets[i][1];
            if (mp.find(from) == mp.end()) {
                priority_queue<string,vector<string>,greater<string> > q;
                q.push(to);
                mp[from] = q;
            } else {
                mp[from].push(to);
            }
        }
        vector<string> res;
        string cur = "JFK";
        dfs(cur, mp, res);
        reverse(res.begin(), res.end());
        return res;
    }

    void dfs(string cur, map<string, priority_queue<string,vector<string>,greater<string> > > &mp, vector<string> &res) {
        while(mp[cur].size()) {
            string nxt = mp[cur].top();
            mp[cur].pop();
            dfs(nxt, mp, res);
        }
        res.push_back(cur);
    }
};