树模型--ID3算法

基于信息增益(Information Gain)的ID3算法

ID3算法的核心是在数据集上应用信息增益准则来进行特征选择，以此递归的构建决策树，以信息熵和信息增益为衡量标准，从而实现对数据的归纳分类。

ID3算法需要解决的问题是如何选择特征作为划分数据集的标准。在ID3算法中，选择信息增益最大的属性作为当前的特征对数据集分类

信息增益

信息增益需要涉及到熵，条件熵这2个概念，先通俗的理解一下：

• 熵：表示随机变量的不确定性。
• 条件熵：在一个条件下，随机变量的不确定性。
• 信息增益：熵 - 条件熵。表示在一个条件下，信息不确定性减少的程度。

比如：太阳明天从东方升起 ，这句话的信息熵等于0，因为这是确定的事件，信息无价值

对于信息增益，举个例子，通俗地讲，假设\(X\)(明天下雨)是一个随机变量，\(X\)的熵假设等于2， \(Y\)(明天阴天)也是随机变量，在阴天情况下下雨的信息熵我们如果也知道的话（此处需要知道其联合概率分布或是通过数据估计）即是条件熵。\(X\)的熵减去\(Y\)条件下\(X\)的熵，就是信息增益。

具体解释：原本明天下雨的信息熵是2，条件熵是0.01（因为如果知道明天是阴天，那么下雨的概率很大，信息量少），这样相减后为1.99就是信息增益。其含义就是在获得阴天这个信息后，下雨信息不确定性减少了1.99，不确定减少了很多，所以信息增益大。也就是说，阴天这个信息对明天下午这一推断来说非常重要。所以在特征选择的时候常常用信息增益，如果IG（信息增益大）的话那么这个特征对于分类来说很关键，决策树就是这样来找特征的。具体到数据集上，信息增益需要结合特征和对应的label来计算。

熵

信息增益与熵(entropy)有关，在概率论中，熵是随机变量不确定性的度量，熵越大，随机变量的不确定性就越大；假设\(X\)是取有限个值的离散随机变量，其概率分布为：

\[P(X=x_i)=p_i,i=1,2,3,...,n
\]

则，熵的定义为：

\[H(X)=-\sum_{i=1}^{n}p_i*\log{p_i}
\]

一般取自然对数\(e\)为底数，值得注意的是，熵实际上是随机变量\(X\)的分布的泛函数，它并不依赖\(X\)的实际取值，而仅仅依赖\(X\)的概率分布，所以它又可以被记作：

\[H(p)=-\sum_{i=1}^{n}p_i*\log{p_i}
\]

其中, \(n\)表示\(X\)的\(n\)种不同的取值, 这个值一般是离散的. \(p_i\)表示为\(X\)取到值为\(i\)的概率.\(log\)一般是自然底数

例子:

条件熵

多个变量的熵叫联合熵, 比如两个变量\(X,Y\)的联合熵就表示为:

\[H(X,Y)=-\sum_{i=1}^{n}p_{(x_i,y_i)}\log p_{(x_i,y_i)}
\]

类似于条件概率,熵同样也存在着条件熵, 条件熵描述了知道某个变量以后, 剩下的变量的不确定性, 其表达式如下:

\[H(X|Y)=-\sum_{i=1}^{n}p_{(x_i,y_i)}\log p(x_i|y_i)
\]

信息增益

\(H(X)\)度量了\(X\)的不确定性, \(H(X|Y)\)度量了知道\(Y\)后,\(X\)的不确定性, 那么\(H(X)-H(X|Y)\)度量的可以理解为:知道\(Y\)的基础上, \(X\)不确定性减少的程度,我们记为\(I(X,Y)\),如图:

更多理解

假定当前样本集合\(D\)中,第\(k\)类样本所占比例为\(p_k(k=1,2,3...,|y|)\), 则\(D\)的信息熵定义为:

\[Ent(D)=-\sum_{k=1}^{|y|}p_k \log p_k
\]

假定离散属性\(a\)有\(V\)个可能的取值\({a^1,a^2...a^v}\), 若使用\(a\)来对样本集进行划分,则会产生\(V\)个分支结点, 也就是说, ID3构建的决策树, 是多叉树, 那么它的信息增益就是

\[Gain(D,a) = Ent(D)-\sum_{v=1}^{V} \frac{|D^v|}{|D|}Ent(D^v)
\]

比如: 一个二分类数据集, 包含17个样本, 其中正例为8,反例为9,那么, 数据集\(D\)的信息熵为:

\[Ent(D)=-(\frac{8}{17}\log \frac{8}{17}+\frac{9}{17}\log \frac {9}{17})
\]

对于变量\(a\),他有三个取值, 那么它可以将数据集划分为三个子集: \(D^1,D^2,D^3\), 其样本里分别为6,6,5, 这三个自数据集中, 正负样本分别为(3,3) (4,2),(1,4), 这三个分支结点的信息熵为为:

\[Ent(D^1)=-(\frac{3}{6} \log \frac{3}{6}+\frac{3}{6} \log \frac{3}{6})
\]

\[Ent(D^2)=-(\frac{4}{6} \log \frac{4}{6}+\frac{2}{6} \log \frac{2}{6})
\]

\[Ent(D^3)=-(\frac{1}{5} \log \frac{1}{5}+\frac{4}{5} \log \frac{4}{5})
\]

那么变量\(a\)的信息增益为:

\[Gain(D,a)=Ent(D)-\sum_{v=1}^{3}\frac{|D^v|}{|D|}Ent(D^v)
\]

ID3 步骤

ID3使用信息增益来决策当前树结点该使用那个变量来构建决策树, 显然,信息增益越大的, 就越能更有效的区分特征(变量)与预测标签之间的关系.

输入\(m\)个样本,每个样本有\(n\)个离散的特征,令特征集合为\(A\),输出决策树\(T\)

• 判断样本是否为同一类别, 如果是, 则返回树T
• 判断特征是否为空, 是, 则返回树T
• 计算A中, 各个特征的信息增益,选择最大的信息增益特征,记为\(i\)
• 按特征\(i\)的不同取值, 将对应的样本分成不同类别,每个类别产生一个子结点,对应的特征值为\(i_j\)
• 重复上述步骤直到结束

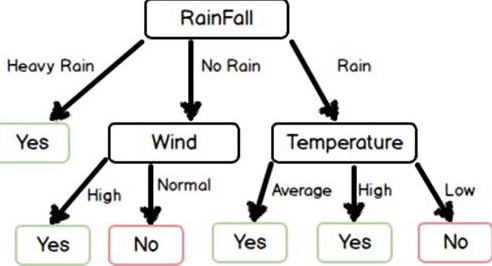
显然，ID3是一个多叉树，且其只能解决分类问题

ID3算法的缺点

1. 无法处理连续的特征，遇到连续的特征的话，就得做连续数据离散化了，可以考虑分桶等策略
2. 采用信息增益更大的特征优先建立决策树, 但相同的数据集下, 取值较多的特征值比取值较少的特征值信息增益更大，即信息增益偏向取值较多的特征。
3. 没有考虑缺失值，当然大部分算法都不支持含有missing value的数据集，尽管理论上算法可以支持，比如gbdt，但大部分gbdt的实现都不支持missing value，目前常用的算法，只有xgb，lgb支持
4. 过拟合问题，id3没有考虑过拟合的对抗策略，相当于是在

ID3算法的优点

1. 可解释性较强