动态规划（三）——线性dp

一.概念

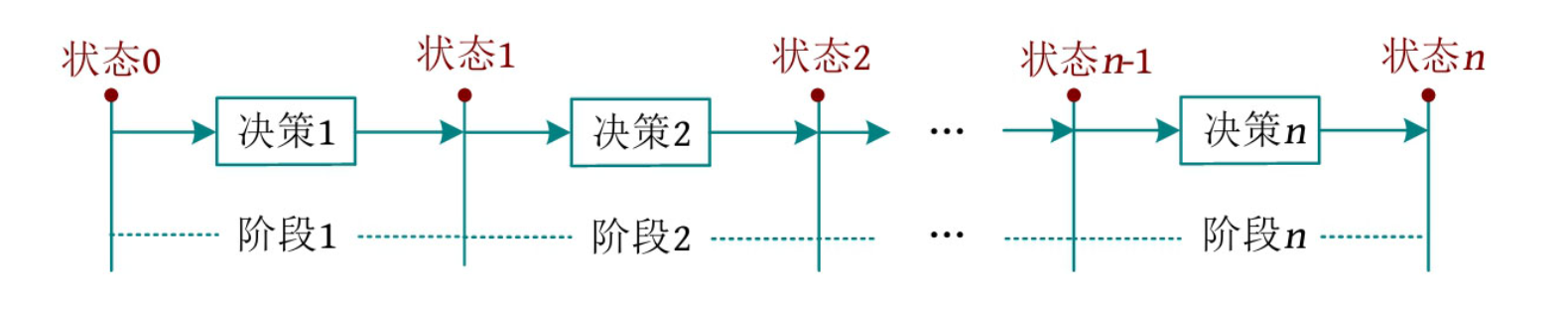
具有线性阶段划分的动态规划算法叫作线性动态规划（简称线性DP）。若状态包含多个维度，则每个维度都是线性划分的阶段，也属于线性DP，如下图所示：

二.线性dp的三大经典例题

1.LIS问题：求最长上升子序列

给定一个长度为N的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式
第一行包含整数N。
第二行包含N个整数，表示完整序列。

输出格式
输出一个整数，表示最大长度。

数据范围
1≤N≤1000，
−10&9≤数列中的数≤109
输入样例：
7
3 1 2 1 8 5 6
输出样例：
4

思路：
确定函数为f[i]表示以第i个数结尾的所有子序列集合，f[i]=最大子序列长度；确定状态转移方程：枚举第i个数前面的数j，如果a[j] < a[i]说明a[j]可能是以a[i]为结尾的最长子序列的倒数第二个数，如果是就用f[j]+1更新f[i]。所以状态转移方程为f[i] = max(f[i], f[j]+1)
时间复杂度O(n2)

代码：

#include <bits/stdc++.h>
using namespace std;
const int N=10010;
int n,a[N],f[N];
int main(){
	cin>>n;
	for(int i=0;i<n;i++) cin>>a[i];
	for(int i=0;i<n;i++){
		f[i]=1;
		for(int j=0;j<i;j++)
			if(a[j]<a[i])
				f[i]=max(f[i],f[j]+1);
	}
	int res=0;
	for(int i=0;i<n;i++) res=max(res,f[i]);
	cout<<res<<endl;
	return 0;
}

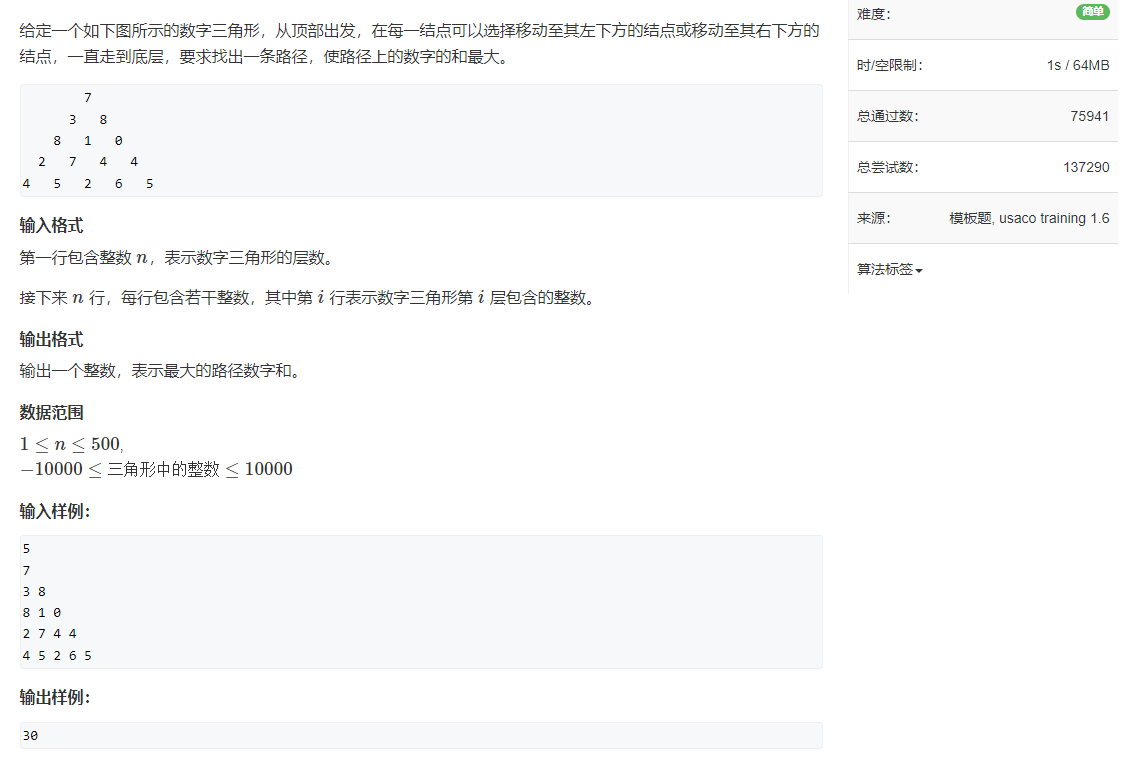
2.LCS问题：数字三角形

代码：

#include <bits/stdc++.h>
using namespace std;
const int N=510;
const int inf=0x3f3f3f3f;
int n,m;
//f[i][j]表示到达第i行j列这个位置的最大值
int a[N][N],f[N][N];
int main(){
	scanf("%d",&n);
	//读入三角形数据
	for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++)
			scanf("%d",&a[i][j]);

	//初始化f
	for(int i=0; i<=n; i++)
		for(int j=0; j<=n; j++)
			f[i][j] = -inf;

	//线性dp
	f[0][0] = 0;
	for(int i=1; i<=n; i++)
		for(int j=1; j<=i; j++)
			f[i][j] = max(f[i-1][j-1], f[i-1][j]) + a[i][j];

	int ans = -inf;
	for(int i=1; i<=n; i++)
		ans = max(ans, f[n][i]);
	printf("%d", ans);
	return 0;
}

3.LCS问题：最长公共子序列

信息学小组截获了两个序列,序列A和B,规定两个序列所隐藏的信息就是两者的最长公共子串
(注意,这里的子串是指连续的,比如说212325233中212是212325233的子串,而213或者223都不是212325233的子串),
现在,他们将这个任务交给你,你要找出这两个序列所隐藏信息的长度

输入格式
两行,A和B(A、B长度均不大于1000,A、B均由0～9之间的数字组成)

输出格式
一个整数为最长公共子串的长度

样例
样例输入
212325233
312123223
样例输出
5

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1000;
char s1[N], s2[N];
int dp[N][N];
int main(){
    cin>>s1+1>>s2+1;// 从1开始存储字符串，方便后续的状态转移
    int len1=strlen(s1+1);
	int len2=strlen(s2+1);
    int ans=0;
    for(int i=1;i<=len1;i++)
        for(int j=1;j<=len2;j++)
            if(s1[i]==s2[j]){
                dp[i][j]=dp[i-1][j-1]+1;//当前字符相等，最长公共子串长度加1
                ans=max(ans,dp[i][j]);
            }
            else dp[i][j]=0;//当前字符不相等，最长公共子串长度为0
    cout<<ans;
    return 0;
}

三.典例之拦截导弹

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：
虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。
某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度（雷达给出的高度数据是不大于30000的正整数，导弹数不超过1000），
计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式
输入只有一行，为若干个正整数，一次为导弹的高度。

输出格式
第一行为最多能拦截的导弹数；
第二行为要拦截所有导弹最少要配备的系统数

样例
样例输入
389 207 155 300 299 170 158 65
样例输出
6
2

核心思想：第一个答案是最长不下降子序列，比较基础，第二个答案是最长上升子序列

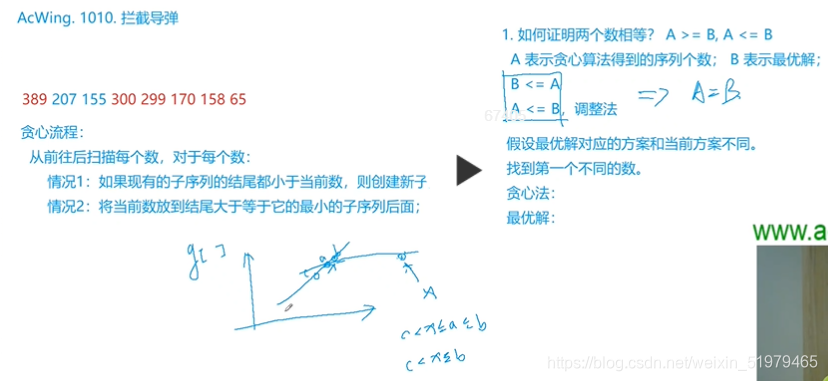
y总讲的非常明白哈，这个是基于贪心的思想，贪心得出一堆子序列，最优解也有一堆子序列
只要证明贪心得出的子序列个数与最优解表示的子序列个数一样就行了，证明方式就是A >= B , A <= B，就可以得出 A == B , 显然A >= B , 因为最优解的子序列数量一定是最少的，现在只需要证明A <= B,首先，两个如果不一样的话必定会有不一样的子序列，这对子序列必定会有第一个不相等的数，贪心的策略就是把他接在现有的子序列结尾最小值的后面，所以现在最优解的这个位置的数一定比他大，所以就可以替换掉，所以子序列的个数是不变的，所以又证明了A >= B，所以A == B,现在怎么用代码实现这个贪心的策略，就只需要维护各个子序列的结尾就行了，对于每一个数无非就两种操作，一种是排在某个序列之后，一种是另外再开辟一个序列，而且由于贪心策略的第二条维护的各个子序列的结尾是单调上升的，用这个序列能将所有导弹全部拦截下来，求最小值的话那么就是求最短上升子序列的个数了

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int f1[N],f[N],a[N];
int main(){
    int n=1,res1=0;
    while(scanf("%d",&a[n])!=EOF) n++;
    for(int i=1;i<n;i++){
        f1[i]=1;
        for(int j=1;j<i;j++){
            if(a[i]<=a[j]) f1[i]=max(f1[i],f1[j]+1);
        }
        res1=max(res1,f1[i]);
    }
    int res2=0;
    for(int i=1;i<n;i++){
        f1[i]=1;
        for(int j=1;j<i;j++){
            if(a[i]>a[j]) f1[i]=max(f1[i],f1[j]+1);
        }
        res2= max(res2,f1[i]);
    }
    cout<<res1<<"\n"<<res2<<endl;
    return 0;
}

如有错误，欢迎大佬们在评论区指正小蒟蒻博主的错误~

#一名爱打篮球的oier#