SPSS统计教程：卡方检验

本文简要的介绍了卡方分布、卡方概率密度函数和卡方检验，并通过SPSS实现了一个卡方检验例子，不仅对结果进行了解释，而且还给出了卡方、自由度和渐近显著性的计算过程。本文用到的数据"2.2.sav"链接为: https://url39.ctfile.com/f/2501739-875711187-f3dbb8?p=2096 (访问密码: 2096)

一.卡方分布

卡方分布是一种概率分布，若\(k\)个随机变量\(Z_1、......、Z_k\)是相互独立且符合标准正态分布的随机变量（数学期望为0、方差为1），那么随机变量\(Z\)的平方和\(X = \sum\limits_{i = 1}^k {Z_i^2}\)被称为服从自由度为\(k\)的卡方分布，记作：\(X \sim {\chi ^2}\left( k \right)\)。

二.卡方概率密度函数

卡方分布的概率密度函数为：

\[{f_x}\left( x \right) = \frac{1}{{{2^{\frac{k}{2}}}\Gamma \left( {\frac{k}{2}} \right)}}{x^{\frac{k}{2} - 1}}{e^{\frac{{ - x}}{2}}}
\]

其中，\(x \ge 0\)，当\(x \le 0\)时\({f_x}\left( x \right) = 0\)，\(\Gamma\)表示Gamma函数。

不同自由度情况下的卡方分布概率密度曲线图：



随着自由度\(k\)的增加，曲线逐渐趋于对称。当自由度\(k\)趋近于无穷时，卡方分布趋近正态分布。

三.卡方检验

卡方检验是非参数检验，以卡方分布为理论依据的假设检验方法，基本原理是通过样本的频数分布来推断总体是否服从某种理论分布。卡方检验的原假设为：样本所属总体的分布与理论分布之间不存在显著差异。卡方检验的检验统计量方程为：

\[{\chi ^2} = \sum\limits_{i = 1}^k {\frac{{{{\left( {{M_{oi}} - {M_{ei}}} \right)}^2}}}{{{M_{ei}}}}}
\]

\(\chi ^2\)统计量在大样本条件下逐渐服从自由度为\(k-1\)的卡方分布，\(M_{oi}\)表示观测频数，\(M_{ei}\)表示理论频数。\({\chi ^2}\)统计量越小，表示观测频数与理论频数越接近。如果小于由显著性水平和自由度确定的临界值，那么认为样本所属的总体分布与理论分布无显著差异。

四.卡方检验例子

实验目的：想知道不同年龄组的样本个数是否存在显著差异。如果\(p>0.05\)，那么接受原假设，即不同年龄组的样本个数并不存在显著不同。

变量视图如下所示：



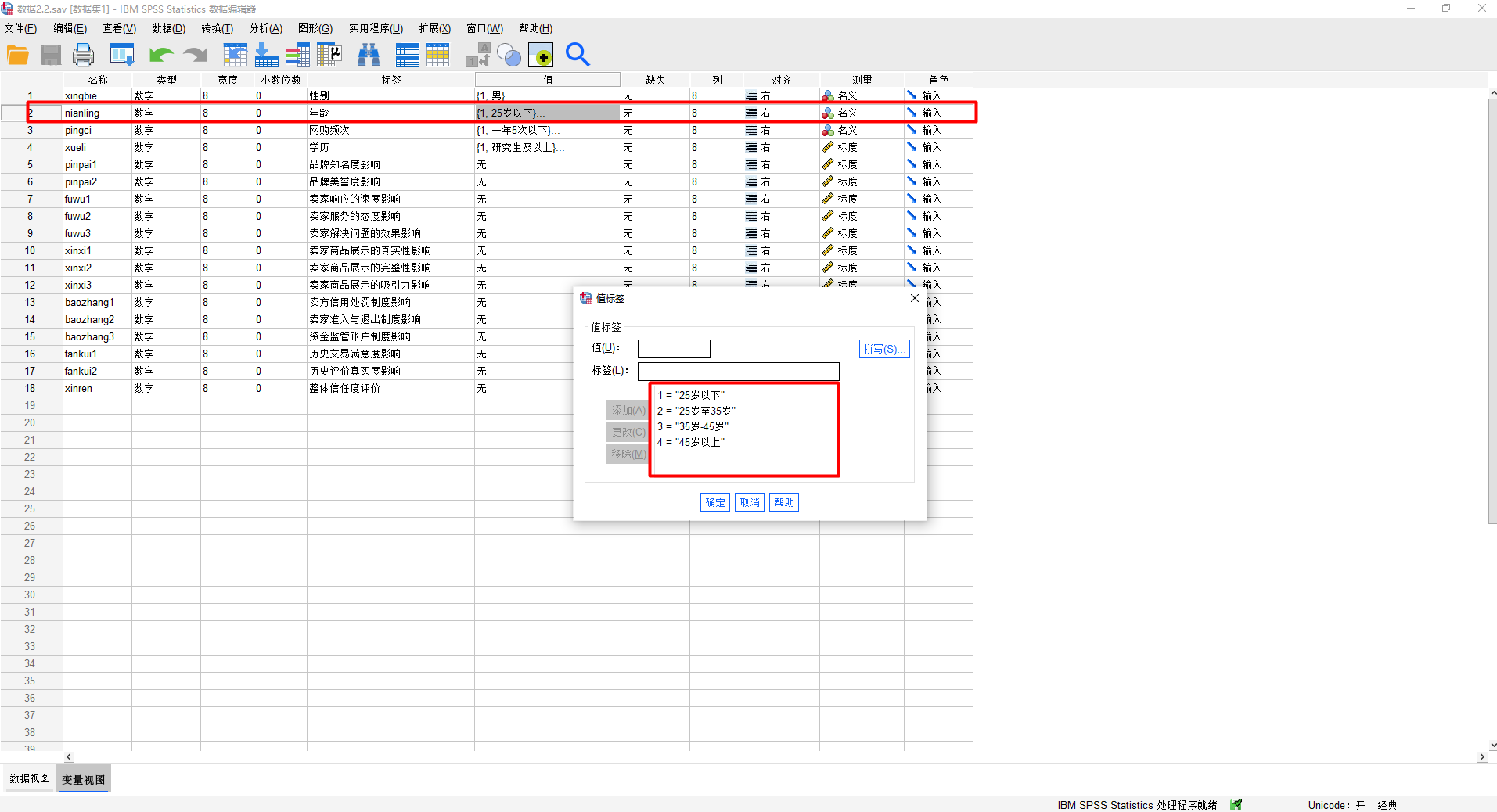
数据视图如下所示：



分析->非参数检验->旧对话框->卡方：



卡方检验结果如下所示：



重点说明下卡方、自由度和渐近显著性是如何计算的：

1.卡方计算

\[\frac{{{{\left( {45 - 50} \right)}^2}}}{{50}} + \frac{{{{\left( {51 - 50} \right)}^2}}}{{50}} + \frac{{{{\left( {52 - 50} \right)}^2}}}{{50}} + \frac{{{{\left( {52 - 50} \right)}^2}}}{{50}} = \frac{{25 + 1 + 4 + 4}}{{50}} = \frac{{34}}{{50}} = 0.68
\]

2.自由度计算

\(k-1\)，\(k\)表示分类变量数。

3.渐近显著性计算

渐近显著性就是\(p\)值，\(p=1-F(卡方值,自由度)\)。使用Python代码计算：

from scipy.stats import chi2
# 第1个参数表示卡方值，第2个参数表示自由度
p = 1 - chi2.cdf(0.68, 3)
print(p) # 0.8778977619609463

在平时看的医学论文中，比较常见的场景是根据卡方检验来计算患者组和对照组的性别是否具有显著性差异：

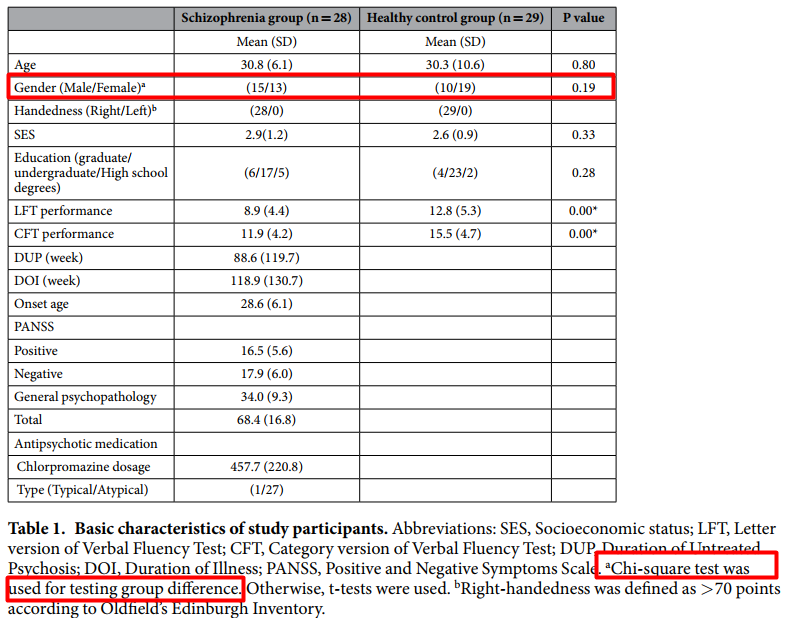
参考文献：

[1]卡方分布：https://zh.wikipedia.org/zh-hans/卡方分布

[2]《SPSS统计分析入门与应用精解》

[3]卡方检验：https://www.ibm.com/docs/zh/spss-statistics/28.0.0?topic=tests-chi-square-test

[4]数据2.2.sav: https://url39.ctfile.com/f/2501739-875711187-f3dbb8?p=2096 (访问密码: 2096)