神经网络优化篇：详解归一化输入（Normalizing inputs）

归一化输入

训练神经网络，其中一个加速训练的方法就是归一化输入。假设一个训练集有两个特征，输入特征为2维，归一化需要两个步骤：

1. 零均值

2. 归一化方差；

   希望无论是训练集和测试集都是通过相同的\(μ\)和\(σ^2\)定义的数据转换，这两个是由训练集得出来的。

第一步是零均值化，\(\mu = \frac{1}{m}\sum_{i =1}^{m}x^{(i)}\)，它是一个向量，\(x\)等于每个训练数据 \(x\)减去\(\mu\)，意思是移动训练集，直到它完成零均值化。

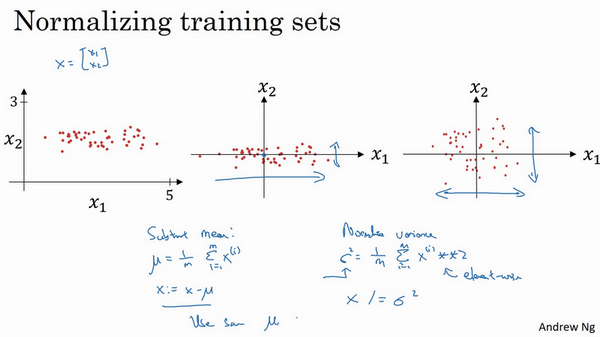
第二步是归一化方差，注意特征\(x_{1}\)的方差比特征\(x_{2}\)的方差要大得多，要做的是给\(\sigma\)赋值，\(\sigma^{2}= \frac{1}{m}\sum_{i =1}^{m}{({x^{(i)})}^{2}}\)，这是节点\(y\) 的平方，\(\sigma^{2}\)是一个向量，它的每个特征都有方差，注意，已经完成零值均化，\(({x^{(i)})}^{2}\)元素\(y^{2}\)就是方差，把所有数据除以向量\(\sigma^{2}\)，最后变成上图形式。

\(x_{1}\)和\(x_{2}\)的方差都等于1。提示一下，如果用它来调整训练数据，那么用相同的 \(μ\) 和 \(\sigma^{2}\)来归一化测试集。尤其是，不希望训练集和测试集的归一化有所不同，不论\(μ\)的值是什么，也不论\(\sigma^{2}\)的值是什么，这两个公式中都会用到它们。所以要用同样的方法调整测试集，而不是在训练集和测试集上分别预估\(μ\) 和 \(\sigma^{2}\)。因为希望不论是训练数据还是测试数据，都是通过相同μ和\(\sigma^{2}\)定义的相同数据转换，其中\(μ\)和\(\sigma^{2}\)是由训练集数据计算得来的。

为什么要这么做呢？为什么想要归一化输入特征，回想一下右上角所定义的代价函数。

\(J(w,b)=\frac{1}{m}\sum\limits_{i=1}^{m}{L({{{\hat{y}}}^{(i)}},{{y}^{(i)}})}\)

如果使用非归一化的输入特征，代价函数会像这样：

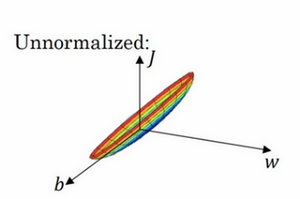
这是一个非常细长狭窄的代价函数，要找的最小值应该在这里。但如果特征值在不同范围，假如\(x_{1}\)取值范围从1到1000，特征\(x_{2}\)的取值范围从0到1，结果是参数\(w_{1}\)和\(w_{2}\)值的范围或比率将会非常不同，这些数据轴应该是\(w_{1}\)和\(w_{2}\)，但直观理解，标记为\(w\)和\(b\)，代价函数就有点像狭长的碗一样，如果能画出该函数的部分轮廓，它会是这样一个狭长的函数。

然而如果归一化特征，代价函数平均起来看更对称，如果在上图这样的代价函数上运行梯度下降法，必须使用一个非常小的学习率。因为如果是在这个位置，梯度下降法可能需要多次迭代过程，直到最后找到最小值。但如果函数是一个更圆的球形轮廓，那么不论从哪个位置开始，梯度下降法都能够更直接地找到最小值，可以在梯度下降法中使用较大步长，而不需要像在左图中那样反复执行。

当然，实际上\(w\)是一个高维向量，因此用二维绘制\(w\)并不能正确地传达并直观理解，但总地直观理解是代价函数会更圆一些，而且更容易优化，前提是特征都在相似范围内，而不是从1到1000，0到1的范围，而是在-1到1范围内或相似偏差，这使得代价函数\(J\)优化起来更简单快速。

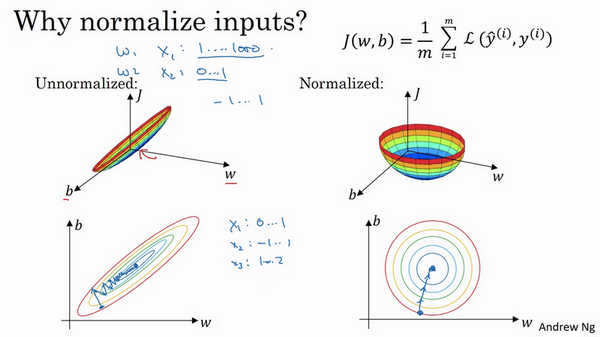
实际上如果假设特征\(x_{1}\)范围在0-1之间，\(x_{2}\)的范围在-1到1之间，\(x_{3}\)范围在1-2之间，它们是相似范围，所以会表现得很好。

当它们在非常不同的取值范围内，如其中一个从1到1000，另一个从0到1，这对优化算法非常不利。但是仅将它们设置为均化零值，假设方差为1，就像设定的那样，确保所有特征都在相似范围内，通常可以帮助学习算法运行得更快。

所以如果输入特征处于不同范围内，可能有些特征值从0到1，有些从1到1000，那么归一化特征值就非常重要了。如果特征值处于相似范围内，那么归一化就不是很重要了。执行这类归一化并不会产生什么危害，通常会做归一化处理，虽然不确定它能否提高训练或算法速度。

这就是归一化特征输入。