hszxoj 矿场搭建 [tarjan]

hszxoj 矿场搭建

• 题目描述
  
  原题来自：HNOI 2012
  
  煤矿工地可以看成是由隧道连接挖煤点组成的无向图。为安全起见，希望在工地发生事故时所有挖煤点的工人都能有一条出路逃到救援出口处。于是矿主决定在某些挖煤点设立救援出口，使得无论哪一个挖煤点坍塌之后，其他挖煤点的工人都有一条道路通向救援出口。
  
  请写一个程序，用来计算至少需要设置几个救援出口，以及不同最少救援出口的设置方案总数。
• 输入格式
  
  输入文件有若干组数据，每组数据的第一行是一个正整数n，表示工地的隧道数，接下来的n行每行是用空格隔开的两个整数a和b，表示挖煤点a与挖煤点b由隧道直接连接。输入数据以0结尾。
• 输出格式
  
  输入文件中有多少组数据，输出文件中就有多少行。每行对应一组输入数据的结果。
  
  其中第i行以 Case i: 开始（注意大小写，Case 与 i 之间有空格，i 与 : 之间无空格，: 之后有空格），其后是用空格隔开的两个正整数，第一个正整数表示对于第i组输入数据至少需要设置几个救援出口，第二个正整数表示对于第i组输入数据不同最少救援出口的设置方案总数。输出格式参照以下输入输出样例。
• 样例输入
  
  9
  
  1 3
  
  4 1
  
  3 5
  
  1 2
  
  2 6
  
  1 5
  
  6 3
  
  1 6
  
  3 2
  
  6
  
  1 2
  
  1 3
  
  2 4
  
  2 5
  
  3 6
  
  3 7
  
  0
• 样例输出
  
  Case 1: 2 4
  
  Case 2: 4 1

解析

一个无向图，故他是有几个vDCC组成的，来讨论每一个vDCC。

先考虑一个问题：
割点是一个很重要的点，如果这个这个vDCC里有割点，说明他可以通过这个割点前往别的vDCC里找出口。

但如果这个割点被砸了，就另外需要安装一个出口跑。

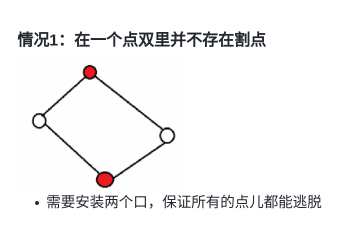
• \(情况1：\)
  
  在一个vDCC里不存在割点，则需安装2个出口。
  
  \(why?\)
  
  若其中一个出口被砸了，需要另一个出口跑。
  
  
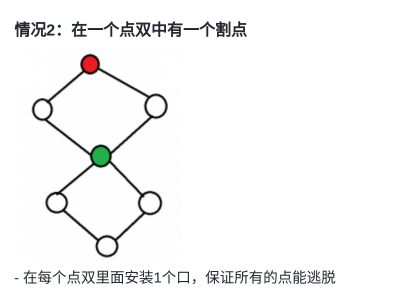
• \(情况2：\)
  
  在一个vDCC中存在一个割点，则需安装1个出口。
  
  \(why?\)
  
  前面说过：\(割点\)是一个很重要的点，如果这个这个vDCC里有割点，说明他可以通过这个割点前往别的vDCC里找出口。
  
  但如果这个割点被砸了，就另外需要安装一个出口跑。
  
  
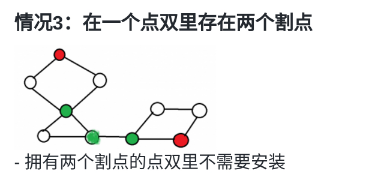
• \(情况3：\)
  
  若一个vDCC里有2个及以上个割点，就什么也不用装了。
  
  比较好理解，参考前面的解释，这个割点被砸了他还有另一个割点可以跑呢。
  
  
  
  \(\Large{参考：}\)
  
  点双通分量(vDCC)
  
  割点
• \(如何实现：\)
  
  ans1（出口个数）上述已解决，那么ans2（方案数）用C这个东西解决一下就可以了。
  • 情况1：\(ans1+=2，ans2+=C(2,n)(=n*(n-1)/2)\);（n指点双内点的个数，n个点里选2个）
  • 情况2：\(ans1++,ans2+=C(1,n-1)(=n-1)\);（除去这个割点，剩下n-1个点里选1个）
  • 情况3：什么都不用做。

代码实现

#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=501;
int dfn[N],low[N],n,ans1,ans2,tot,a,b,num,t;
bool cut[N];
vector<int>e[N],dcc[N];
stack<int>s;
template<typename Tp> inline void read(Tp&x)
{
    x=0;register bool f=1;
    register char c=getchar();
    for(;c<'0'||c>'9';c=getchar()) if(c=='-') f=0;
    for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
    x=(f?x:~x+1);
}
void clean()
{
    memset(dfn,0,sizeof(dfn)),
    memset(low,0,sizeof(low)),
    memset(cut,0,sizeof(cut)),
    memset(e,0,sizeof(e)),
    memset(dcc,0,sizeof(dcc)),
    ans1=tot=num=0,ans2=1;
}
void tarjan(int x,int fa)
{
	dfn[x]=low[x]=++tot;
	s.push(x);
    int child=0;
	if(x==fa&&e[x].size()==0)
	{
		dcc[++num].push_back(x);
		return ;
	}
	for(int y:e[x])
		if(!dfn[y])
		{
			tarjan(y,fa);
			low[x]=min(low[x],low[y]);
			if(low[y]>=dfn[x])
			{
				++num,++child;
                if(x!=fa||child>1) cut[x]=1;
				int z;
				while(z!=y)
					z=s.top(),
					s.pop(),
					dcc[num].push_back(z);
				dcc[num].push_back(x);
			}
		}
		else low[x]=min(low[x],dfn[y]);
}
signed main()
{
	#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif
	while(1)
    {
        read(n);
        if(n==0) return 0;
        clean();
        for(int i=1;i<=n;i++)
            read(a),read(b),
            e[a].push_back(b),
            e[b].push_back(a);
        for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,i);
        for(int i=1;i<=num;i++)
        {
            int tge=0,l=dcc[i].size();
            if(l==1) continue;//他可能是森林qwq
            for(int j=0;j<l;j++) if(cut[dcc[i][j]]) tge++;
            if(tge==0) ans1+=2,ans2*=l*(l-1)/2;
            else if(tge==1) ans1++,ans2*=l-1;
        }
        cout<<"Case "<<++t<<": "<<ans1<<' '<<ans2<<endl;
    }
}

重要注意

数据可能是森林，及他是存在孤点的（没有爸爸也没有儿子的孤儿），非常的可怜，如果他这个点双被砸了（这个点双里只有他这一个可怜的孩子），那么他已经死了 \(\Large{qwq}\) ，没有去拯救他的必要了，所以孤点不需要安装出口，需特殊考虑。



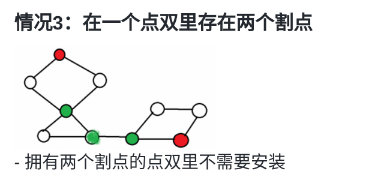
右边这个小东西就是孤点，与左边这个大家伙构成了一个森林。