【LeetCode排序专题02】最小k个数，关于快速排序的讨论

最小k个数

https://leetcode.cn/problems/smallest-k-lcci/

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

示例 1：

输入：arr = [3,2,1], k = 2

输出：[1,2] 或者 [2,1]

示例 2：

输入：arr = [0,1,2,1], k = 1

输出：[0]

限制：

0 <= k <= arr.length <= 10000

0 <= arr[i] <= 10000

快速排序

快排是一种冒泡法的优化版本，逻辑上使用了分治思想，代码实现上使用了递归的方式，直接上例子来说

以下是一个无序数组，使用快排对其进行排序，核心代码逻辑如右侧所示

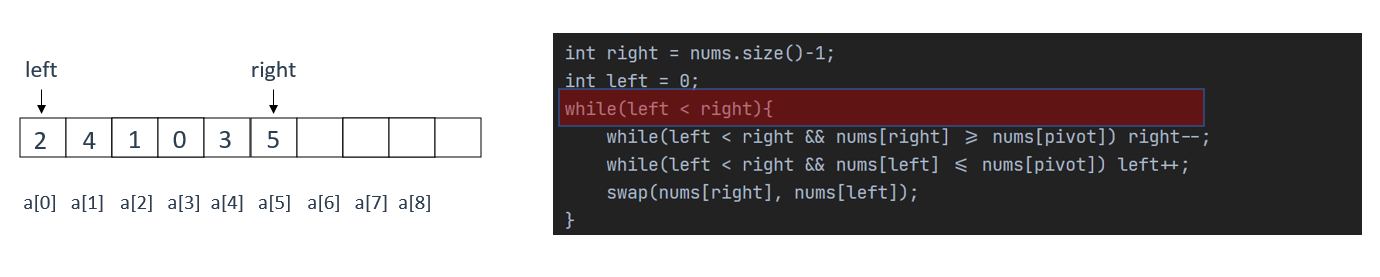
默认以left初始时指向的最左侧元素为基准值

基准值也称为pivot，即"轴"。不断移动左右指针，与轴比较，比轴大的放在轴的右边，比轴小的放在轴的左边

在这里，pivot = 2，即nums[0]

此时满足最外层循环条件，进入循环

大循环内还有两个循环，用于移动左右指针

当前右指针大于基准值pivot（5 > 2），移动right，到3处，还是大，继续移动

到0处不满足条件，执行下一个小循环，判断左指针移动情况

当前左指针等于基准值pivot（2 = 2），满足第二个小循环条件，移动left

此时左指针等于4，大于基准值2，退出小循环，继续执行后面的语句

此时，将左右指针指向的值进行交换

当前左右指针并没有相交，因此继续执行大循环内的两个小循环

（后面的过程同理，就不画图了）

右指针的值还是大于pivot，right左移

此时不满足条件，往后执行第二个小循环

左指针的值小于pivot（0 < 1），left右移

左右指针相交，大循环结束，此时两指针相交的位置就是当前pivot需要移动到的位置

如图所示，pivot（2）移动到相交处

此时，我们就以pivot为基准对数组进行了第一次划分

总结一下过程：

1、先确定基准值，一般用数组最左边的值。

2、然后用右指针和基准值比较，如果右指针指向的值大就不用动当前指向值，向左移动右指针，继续比较，直到右指针指向的值小于基准值（注意，此时还不能交换左右指针值），开始移动左指针

3、使用左指针的值与基准值比较，如果左指针指向的值小就不用动当前指向值，向右移动左指针，继续比较，直到左指针指向的值大于基准值，此时再交换左右指针的值

4、完成一轮移动，如果当前左右指针相交了就结束循环，最左边的基准值和当前相交位置的值互换

5、此时数组被分为左右区间，分别在这两个区间触发递归，继续排序

可见，关键点在于：一定要右指针、左指针都移动完毕之后再交换左右指针指向的值，然后再判断左右指针是否相交

继续

当前，pivot（2）左边的都是小于2的数，pivot（2）右边的都是大于2的数

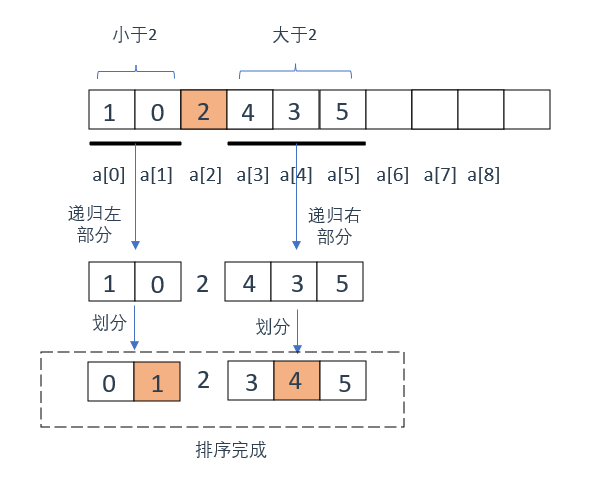
然后，对当前pivot划分的左右区间再次进行划分（方法相同）

这里就是快排需要使用递归的原因，我们需要不断的划分剩余的区间，直到最后排好序

下面来看代码实现

代码分析

凡是涉及递归的都可以按照三部曲来写

1、确认递归函数的参数和返回值

这里是对数组进行排序操作，不需要返回值；

输入参数为待排序的数组以及需要排序的区间

class Solution {
private:
    //对数组进行排序操作，不需要返回值,输入参数为待排序的数组以及需要排序的区间
    void quickSort(vector<int>& arr, int left, int right){

    }
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {

    }
};

2、确定终止条件

终止条件肯定是左右指针相交

class Solution {
private:
    //对数组进行排序操作，不需要返回值,输入参数为待排序的数组以及需要排序的区间
    void quickSort(vector<int>& arr, int left, int right){
        //确定终止条件
        if(left > right) return;
    }
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {

    }
};

3、处理单层递归逻辑

在代码实现时，我们可以直接将left指针指向的值视为pivot（也就是说不用单独定义一个pivot变量，一是影响性能，二是在交换变量时容易逻辑混乱）

循环之前，定义两个循环变量i、j分别初始化为left和right的值

class Solution {
private:
    //对数组进行排序操作，不需要返回值,输入参数为待排序的数组以及需要排序的区间
    void quickSort(vector<int>& arr, int left, int right){
        //确定终止条件
        if(left >= right) return;

        //处理单层逻辑
        //单独定义循环变量
        int i = left, j = right;
        // int pivot = left;//不用多余再定义一个变量
        while(i < j){
            //右指针指向的数要大于基准值的话就不用动，仅移动指针(此时，基准值由left充当)
            while(i < j && arr[j] >= arr[left]) j--;
            while(i < j && arr[i] <= arr[left]) i++;//同理
            swap(arr[i], arr[j]);//不满足上述条件就交换
            //将right指向的但是小的数放到pivot左边，将left指向的但是大的数放到pivot右边
        }//大循环结束，此时左右指针相交，把pivot移动到相交位置
        swap(arr[i], arr[left]);//写j也行

        //此时已经将数组分为左区间（小于pivot）和右区间（大于pivot）
        //调用递归对左右区间再次进行划分，直到排序完成
        quickSort(arr, left, i - 1);//左区间递归排序(左指针left重置为数组最左边元素)
        quickSort(arr, i + 1, right);//右区间递归(右指针right重置为数组最右边元素)
    }
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {

    }
};

完整代码

class Solution {
private:
    //对数组进行排序操作，不需要返回值,输入参数为待排序的数组以及需要排序的区间
    void quickSort(vector<int>& arr, int left, int right){
        //确定终止条件
        if(left >= right) return;

        //处理单层逻辑
        int i = left, j = right;
        // int pivot = left;//不用多余再定义一个变量
        while(i < j){
            //右指针指向的数要大于基准值的话就不用动，仅移动指针(此时，基准值由left充当)
            while(i < j && arr[j] >= arr[left]) j--;
            while(i < j && arr[i] <= arr[left]) i++;//同理
            swap(arr[i], arr[j]);//不满足上述条件就交换（即右指针、左指针按顺序移动完毕）
            //将right指向的但是小的数放到pivot左边，将left指向的但是大的数放到pivot右边
        }//大循环结束，此时左右指针相交，把pivot移动到相交位置
        swap(arr[i], arr[left]);//写j也行

        //此时已经将数组分为左区间（小于pivot）和右区间（大于pivot）
        //调用递归对左右区间再次进行划分，直到排序完成
        quickSort(arr, left, i - 1);//左区间递归排序(左指针left重置为数组最左边元素)
        quickSort(arr, i + 1, right);//右区间递归(右指针right重置为数组最右边元素)
    }
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        //调用递归函数
        quickSort(arr, 0, arr.size() - 1);
        vector<int> res(arr.begin(), arr.begin() + k);//排序后，取数组中"前k大的元素"构成结果数组

        return res;
    }
};

优化版

这里其实有个可以优化的点

在每次划分完毕后，基准值都会在arr[i]的位置（i为循环变量）

因为题目要求是：返回数组中“前k个最小的数”，只要返回就行，这些数有无顺序均可以

因此可以根据k与i的关系来决定是否继续排序

• 若k < i，代表第 k + 1 小的数字在 左子数组 中，则递归左子数组
• 若k > i，代表第 k + 1 小的数字在 右子数组 中，则递归右子数组
• 若k = i，代表此时 arr[k] 即为第 k + 1小的数字，则直接返回数组前 k 个数字即可;

在代码上，需要把递归函数的返回值改为数组，因为要依据i与k的大小关系来决定递归左区间还是右区间，并且，k也需要作为参数输入到递归函数中

TBD