4.3 省选模拟赛 序列游戏 dp

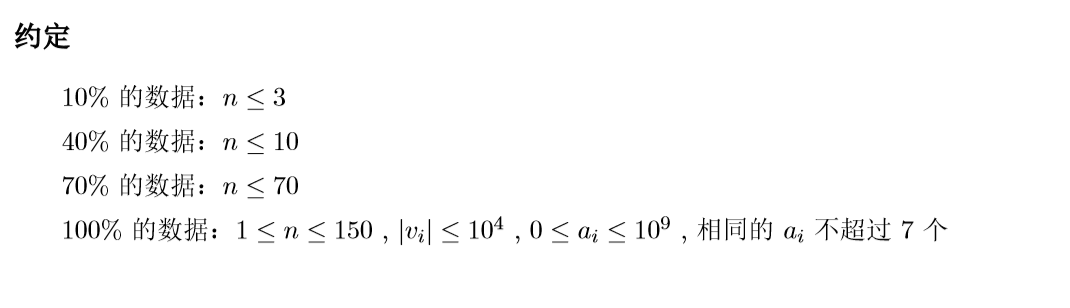
可以发现 某一段被删除后状态难以表示 也难以链接起来。

考虑暴力 有40分的状压dp 暴力存状态 然后枚举转移即可。最后注意和f[0]这个状态取max 不然一分都没有。

const int MAXN=12;
int f[1<<MAXN];
int a[MAXN],b[MAXN],v[MAXN],w[MAXN];
int n,maxx,ans;
int main()
{
	freopen("1.in","r",stdin);
	//freopen("sequence.out","w",stdout);
	get(n);
	if(n<=10)
	{
		memset(f,0xcf,sizeof(f));
		rep(1,n,i)get(v[i]);
		rep(1,n,i)get(a[i]);
		maxx=(1<<n)-1;
		f[maxx]=0;
		fep(maxx,1,i)
		{
			if(f[i]<-INF)continue;
			int top=0;
			rep(1,n,j)if((i&(1<<(j-1))))b[++top]=a[j],w[top]=(1<<(j-1));
			rep(1,top,j)
			{
				rep(1,top-j+1,k)
				{
					int en=k+j-1;
					int flag=0,s=i;
					rep(k,en,l)
					{
						if(l>k)
						{
							if(abs(b[l]-b[l-1])!=1){flag=1;break;}
							if(l<en)if(b[l]<b[l-1]&&b[l]<b[l+1]){flag=1;break;}
						}
						s=s^w[l];
					}
					if(!flag)f[s]=max(f[s],f[i]+v[j]);
				}
			}
			ans=max(ans,f[i]);
		}
		ans=max(ans,f[0]);
		put(ans);return 0;
	}
}

从上面的分析我们也可以发现难点就在于状态的表示。

正解：int f[N][N][N],g[N][N][N],last[N][N];//f[i][j][k]表示对于区间[i,j] j一定和后面的K个连成一段进行删除的最大值.

//f数组表示可能存在单个高峰 g数组和f组一样 g数组表示没有峰为单调序列。形状定义为[i,j-1]形成的形状

很遗憾不明白为什么要这样做 也看不懂这样的转移是再干嘛。

留下STD 以后填坑。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <map>
using namespace std;

const int N = 153, INF = -0x3f3f3f3f;
int n, m, ans[N], v[N], a[N], last[N][N], f[N][N][N], g[N][N][N];
map<int, int> hash;

inline void upt(int &x, const int &y) {
	if (x < y) x = y;
}

char ch;
inline int read() {
	int res = 0, sgn = 0;
	while (ch = getchar(), ch < '0' || ch > '9') if (ch == '-') break;
	ch == '-' ? sgn = 1 : res = ch - 48;
	while (ch = getchar(), ch >= '0' && ch <= '9') res = res * 10 + ch - 48;
	return sgn == 0 ? res : -res;
}

int main() {
  freopen("1.in", "r", stdin);
 // freopen("sequence.out", "w", stdout);

	n = read();
	for (int i = 1; i <= n; ++i) v[i] = read();
	for (int i = 1; i <= n; ++i) {
		a[i] = read();
		if (hash[a[i]] == 0) hash[a[i]] = ++m;
	}
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j) last[i][j] = last[i - 1][j];
		last[i][hash[a[i]]] = i;
	}
	memset(f, INF, sizeof(f));
	memset(g, INF, sizeof(g));
	//cout<<f[0][0][0]<<' '<<INF<<endl;
	for (int i = 1; i <= n; ++i) {
		for (int j = 0; j <= n; ++j)
			if (i + j <= n)
				f[i][i][j] = g[i][i][j] = v[j + 1];
			else 	break;
		f[i][i - 1][0] = g[i][i - 1][0] = 0;
	}
	for (int l = 1; l <= n; ++l)
		for (int i = 1; i <= n; ++i) {
			int j = i + l;
			if (j > n) break;
			for (int k = 0; k <= n; ++k) {
				if (j + k > n) break;
				upt(f[i][j][k], f[i][j - 1][0] + v[k + 1]);
				upt(g[i][j][k], f[i][j - 1][0] + v[k + 1]);
				int p = hash[a[j] + 1], q = hash[a[j] - 1];
				for (int h = last[j][p]; h >= i; h = last[h - 1][p])
					upt(f[i][j][k], f[i][h][k + 1] + f[h + 1][j - 1][0]);
				for (int h = last[j][q]; h >= i; h = last[h - 1][q]) {
					upt(f[i][j][k], g[i][h][k + 1] + f[h + 1][j - 1][0]);
					upt(g[i][j][k], g[i][h][k + 1] + f[h + 1][j - 1][0]);
				}
			}
		}
	ans[0] = 0;
	for (int i = 1; i <= n; ++i) {
		upt(ans[i], ans[i - 1]);
		for (int j = 0; j < i; ++j)
			upt(ans[i], ans[j] + f[j + 1][i][0]);
	}
	printf("%d\n", ans[n]);
	return 0;
}