Codeforces Round #651 (Div. 2) A. Maximum GCD (思维)

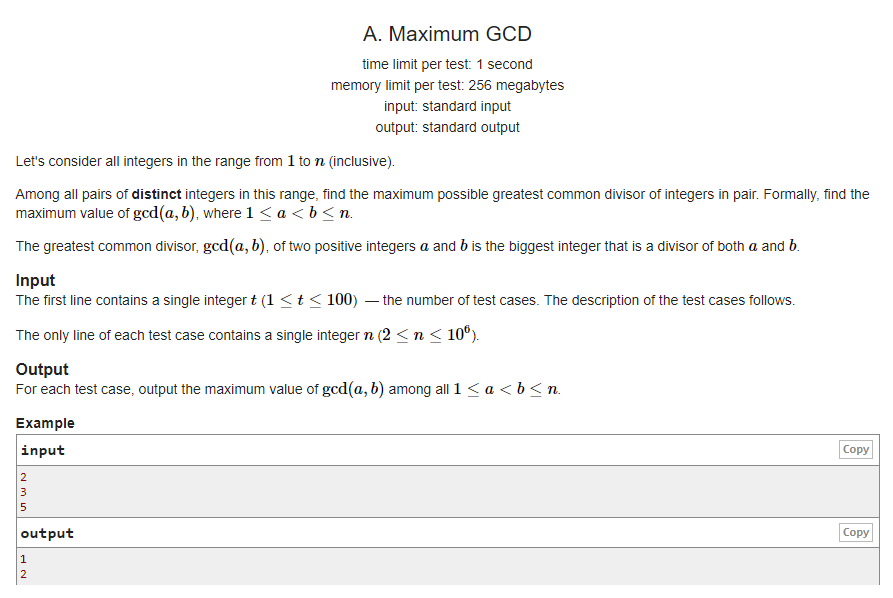
• 题意:在\(1\)~\(n\)中找两个不相等的数使得他们的\(gcd\)最大.

• 题解:水题,如果\(n\)是偶数,那么一定取\(n\)和\(n/2\),\(n\)是奇数的话,取\(n-1\)和\((n-1)/2\).

• 代码:

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  
  int t;
  int n;
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
  	cin>>t;
  	 while(t--){
  	 	cin>>n;
  	 	if(n%2==0){
  	 		cout<<n/2<<endl;
  	 	}
  	 	else{
  	 		cout<<(n-1)/2<<endl;
  	 	}
  	 }
  
      return 0;
  }