B树摘要

BTree

以下内容是根据《算法导论》摘要而来，由于国内书籍对B树的定义是以阶来定义，而《算法导论》中使用的是最小度来定义，并且节点中关键字个数也不相同，在翻看网上博客时，产生了诸多疑问，考虑到B树是从国外而来，我还是打算相信《算法导论》

定义

• 用最小度来t定义,t>=2,每个节点的关键字个数 t-1 < n < 2t-1，非叶子节点子女指针个数范围 t < c <2t (有j个孩子的节点，恰好有j-1个关键字)
• 非叶子节点上也有数据，适合随机检索，越靠近root，磁盘i/o时间越少，速度越快
• 所有叶子节点具有相同的深度，根节点至少有一个关键字
• 真实数据并未存放到B树的各个节点上，节点上只是存储了节点数据在硬盘上的存储地址
• 通常采用的分支因子为50-2000，主要取决于一个关键字相对于一个磁盘块|内存页的大小
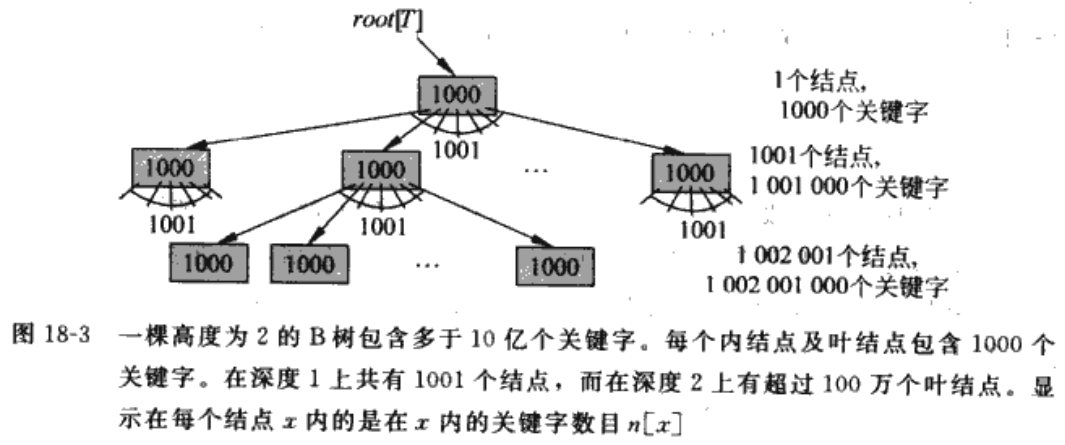
• 由于根节点实现时，会一直在主存中，寻找某个关键字（仅寻找关键字，应该不含数据那一次），进行的磁盘IO次数，最多为树的高度（高度h为树的层数-1）,树的深度与根节点为第几层有关，如根节点为0，则层数为3的树，深度为2，如果根节点为1，则深度为3
• 一颗分支因子为1001，高度为2的树，可以有10亿个关键字
• 每个页节点有相同的高度
• 树非空时，root至少含义一个关键字

搜索

实现search操作时，会用到递归

顶层调用为search(root,k)

search(node,k)

i=1

while(k> keys[i])

i++;

if(keys[i] =k)

then return (node,i)

if(leaf[i] == null)

then return null

else disk-read(leaf[i])

then return search(leaf[i],k)

时间复杂度O(tlogt(n))

插入

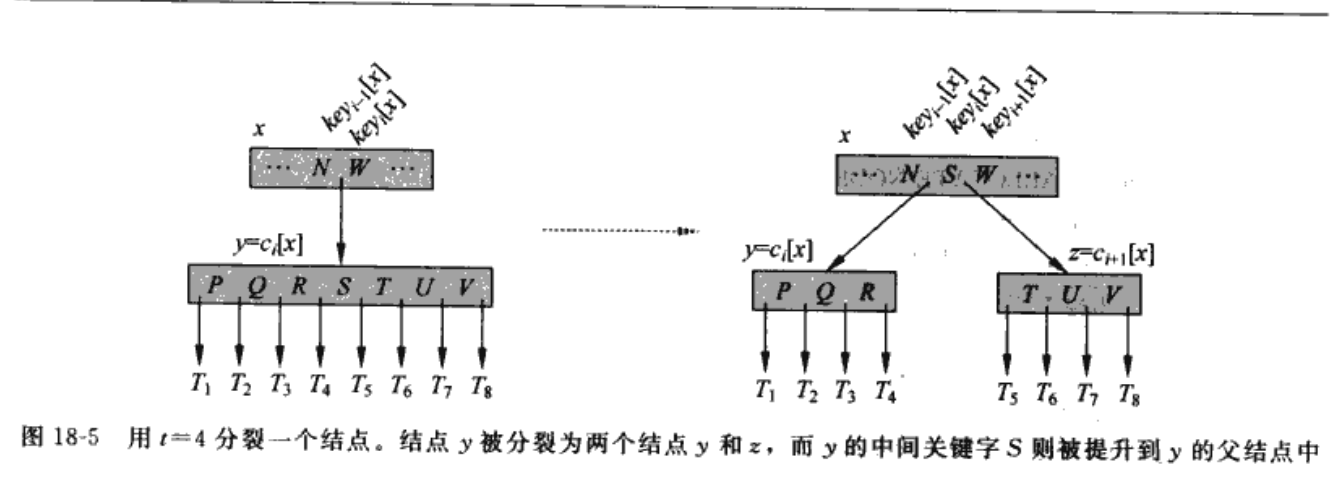
以最小度为4举例，节点的关键字个数为 3~7

• 如果k需要插入node x，而x不是叶节点，则应将k插入到x的子树中去，直到找到叶节点

• 判断是否需要分裂，确保无满子节点->如果插入前节点中key的个数为7（即判断是否满子）,则不能再插,因为它已经达到了最大key个数，此时需要将这个节点分裂，方法是将中间关键字上移到父节点，上移后，一个节点分裂为2个节点，左边的是小于中间key的关键字，右边是大于中间key的关键字，建立一个新的节点，使之继续满足要求，以此类推，如果中间key上移到父节点后，父节点的key大于7，则父节点按次方法继续分裂，最终可能导致根节点分裂，这样，树的高度就会 + 1，根节点分裂是B树高度增加的唯一途径

• 判断k需要插入到分裂后（如果需要分裂的话）的哪个叶子节点

• 递归插入操作，在任何时刻，需要留在主存中的页面数为O(1),注:根节点以外，根结点始终在主存中

删除

删除操作和插入操作一样，为了满足B树的性质，需要尝试合并节点，而插入操作会分裂节点

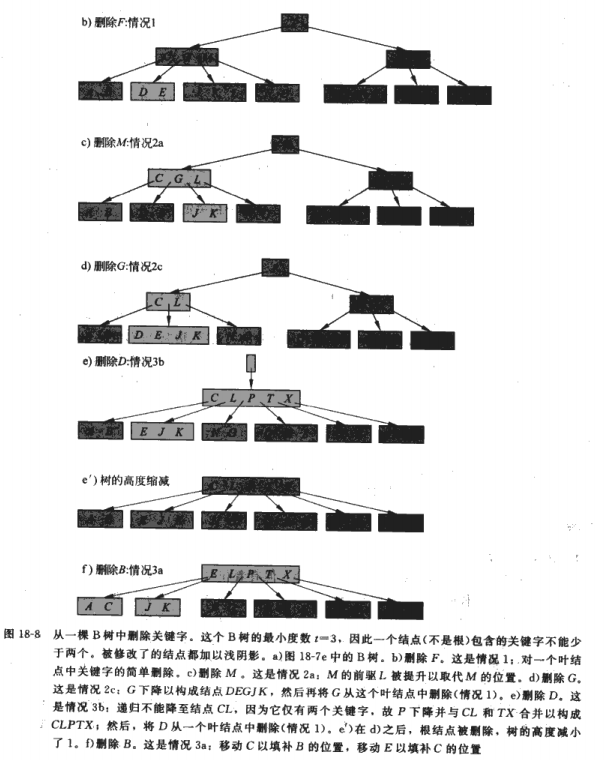
• 1.如果关键字k在叶子节点中，直接删除；

• 2.如果在内部节点中，则判断节点中，前于k的子节点p中关键字的个数至少有t个关键字，此时将其最大的键提到k的位置；

• 3.否则判断后于k的子节点中关键字个数大于t，如果大于，将其最小的键提到k的位置，这样树的结构变化就很小，仅需要修改几个指针

• 4.如果前于k的子节点和后于k的子节点都只有t-1个关键字，则将他们3个合并到前于k的节点上去

• 5.不在某个节点中，递归查询，查询中如果遇到相邻节点关键字较少时，将其合并，合并操作可能会导致根节点下沉，高度

• 6.k不在某个内节点中(k实际在树结构中)，此时需要递归的寻找它，并且在递归寻找中，如果发现含关键字的子树的根，只有t-1个关键字，则通过移动它兄弟节点中的关键字，来保证它至少有t个关键字（至少t个关键字的原因由1.2.3点可以得知，是为了在将来的删除操作来临时，有较大概率命中1.2.3）。

• 如果根结点不含有任何关键字，但它有子节点，则需要删除根结点，从而使树的高度降低了1

这其中最重要的是第5点，它从根节点开始，会遍历所有子树中含k的节点，如果节点中不至少包含t个关键字，则会进行操作5，当删除操作以此方式操作完整个树后，树的高度可能-1;