Acwing 120. 防线

题目地址

题目简译：给定\(n\)个等差数列，每个等差数列的起点为\(s\)，终点为\(e\)，差为\(d\)。整个序列中至多有一个位置所占数字是奇数。判断奇数位是否存在，如果不存在输出"There's no weakness."，如果存在输出位置与大小。

温馨提示：\(⌊x⌋\)为将\(x\)向下取整

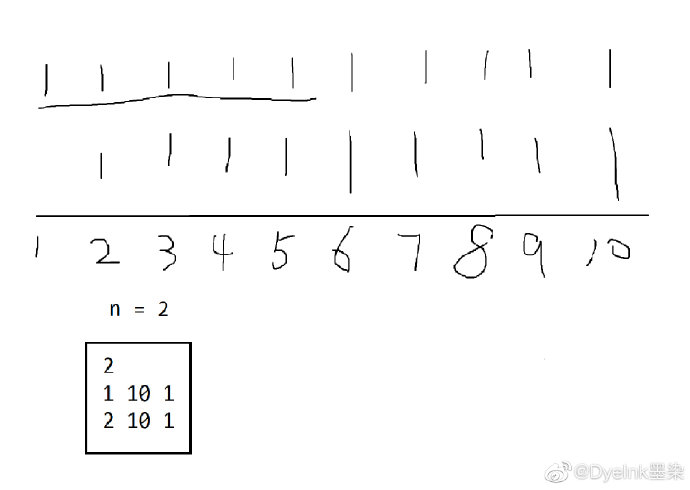
算法：前缀和 + 二分位置

1、奇数位存在性

整个序列中至多有一个位置的数字所占数量是奇数，所以如果存在奇数位，则整个数列的总和必然是奇数（奇数 + 偶数 = 奇数，偶数 + 偶数 = 偶数）。反之，若不存在奇数位，则一定是偶数。故只需判断数字数量的总和的奇偶性即可。

2、二分位置

若存在这个奇偶性，我们可以通过二分答案的位置来找到这个位置，然后判断区间\([l,mid]\)的总和的奇偶性。若为奇数，则奇数位存在于此区间。反之若为偶数，则一定存在于\([mid+1,r]\)区间。用这个方法逐步缩小范围即可。

关于查找\([l,mid]\)的总和，我们可以用前缀和的思路，用\(sum[n] - sum[mid-1]\)即可求出。(\(sum[i]\)为求出\(i\)位置之前所有位置的和)

3、\(O(n)\)时间求出区间\(sum[x]\)的数字个数

设整个数列的最小位置为\(minn\)

这里，我们枚举每一个等差数列（它的起点为\(s\)，终点为\(e\)，差为\(d\)）。若\(s <= x\)，则两区间存在交集。

则它与\([minn,x]\)的共同区间为\([s,min(e,x)]\)。那么此区间包含此数列的个数是\((⌊(min(e,x) - s) / d⌋ + 1\)。

正确性证明十分容易：

在此区间中存在一段区间，共\(⌊s,min(e,x) / d⌋ * d\)个位置，头尾的位置上都有数字，差为\(d\)，则数字的数量就是\((⌊(min(e,x) - s) / d⌋ + 1\)。

时间复杂度：\(O(nlogn)\)

二分的时间为\(O(logn)\)，每次\(check()\)的时间为\(O(n)\)，故总的时间复杂度为\(O(nlogn)\)。

C++ 代码

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
const int N = 200000 + 1, INF = 1e9;
int t,n;
struct node{
	int s,e,d;
}a[N];
int getSum(int x){ // O(n) 求[1,x]的前缀和
	int res = 0;
	for(int i = 1; i <= n; i++)
		if(a[i].s <= x)
			res += (min(a[i].e, x) - a[i].s)/a[i].d + 1;

	return res;
}
bool check(int l,int r){ // O(n) 查找[l,r]是否存在奇数位
	return (getSum(r) - getSum(l - 1)) & 1;
}
int main(){
	cin >> t;
	while(t--){
		cin >> n;
		int maxn = -INF, minn = INF;
		for(int i = 1; i <= n; i++){
			cin >> a[i].s >> a[i].e >> a[i].d;
			minn = min(minn,a[i].s);
			maxn = max(maxn,a[i].e);
		}

		if(!(getSum(maxn) & 1)){
			cout << "There's no weakness." << endl;
		}else{
			int l = minn, r = maxn;
			while(l <= r){
				int mid = (l + r) >> 1;
				if(check(l,mid))r = mid - 1;
				else l = mid + 1;
			}

			cout << l << " " << (getSum(l) - getSum(l - 1)) << endl;
		}
	}
	return 0;
}