图的深度优先遍历算法（DFS）

搜索算法有很多种，本次文章主要分享图（无向图）的深度优先算法。深度优先算法（DFS）主要是应用于搜索中，早期是在爬虫中使用。其主要的思想有如下：

1.先访问一个节点v，然后标记为已被访问过
2.找到第一个节点的邻接节点w
3.如果第一个邻接节点w存在就走第4步，如果不存在就返回第一个节点v,从v的其他节点继续开始
4.如果节点w存在就怕判断该节点是否被访问过，如果没有被访问过就进行升读优先遍历(重复1，2，3)
5.查找节点v的邻接节点w的邻接节点（继续执行3）

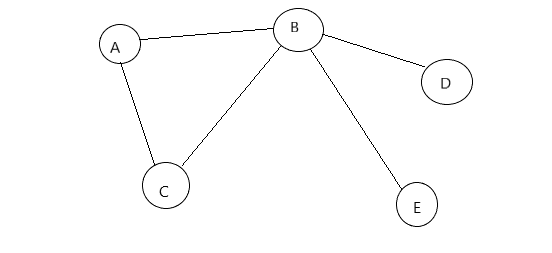
先创建一个图，主要使用邻接矩阵（二位数组）进行存储节点到节点之间的关系。如果A可以到达B那么用1表示，不可以就用0进行表示。

而二维数组的长度是节点的个数，列如有n个节点那么二位数组的长度为Array[n][n]。

创建图以及深度优先算法的代码如下：

  1 public class Graph {
  2
  3     //创建一个集合用来存放顶点
  4     private ArrayList<String> arrayList;
  5     //创建一个二位数组来作为邻接矩阵
  6     private int[][] TwoArray;
  7     //边的数目
  8     private int numOfEdges;
  9     //使用一个数组记录节点是否被访问过
 10     private boolean[] isVisted;
 11     public static void main(String[] args) {
 12         Graph graph = new Graph(5);
 13         //测试
 14         String[] ver={"A","B","C","D","E"};
 15         //将节点放到集合中
 16         for (String s : ver) {
 17          graph.InsertVex(s);
 18         }
 19         //设置边
 20         //A-B A-C B-C B-D B-E
 21         graph.InsertEdeges(0,1,1);
 22         graph.InsertEdeges(0,2,1);
 23         graph.InsertEdeges(1,2,1);
 24         graph.InsertEdeges(1,3,1);
 25         graph.InsertEdeges(1,4,1);
 26         //显示
 27         graph.Show();
 28         graph.DFS();
 29     }
 30
 31     //初始化数据
 32     public Graph(int n){
 33         arrayList=new ArrayList<>(n);
 34         TwoArray=new int[n][n];
 35         numOfEdges=0;
 36         isVisted=new boolean[n];
 37     }
 38
 39     /**
 40      * 根据节点的下标返回第一个邻接节点的下标
 41      * @param index 节点的下标
 42      * @return
 43      */
 44     public int getFirstVex(int index){
 45         for (int i = 0; i < arrayList.size(); i++) {
 46             if(TwoArray[index][i]!=0){
 47                 return i;
 48             }
 49         }
 50         return -1;
 51     }
 52
 53     /**
 54      * 根据前一个节点下标获取下一个节点的下标
 55      * @param v1 找到的第一个节点的
 56      * @param v2 找到的第一个邻接节点并且被访问过的
 57      * @return
 58      */
 59     public int getNextVex(int v1,int v2){
 60         for (int i = v2+1; i < numEdges(); i++) {
 61             if(TwoArray[v1][i]!=0){
 62                 return i;
 63             }
 64         }
 65         return -1;
 66     }
 67
 68     /**
 69      * 深度优先算法的实现
 70      * @param isVisted
 71      * @param i
 72      */
 73     public void DFS(boolean[] isVisted,int i){
 74         //先访问该节点
 75         System.out.print(getValue(i)+"->");
 76         //将节点设置为已经访问
 77         isVisted[i]=true;
 78         //查找该节点的第一个邻接节点
 79         int firstVex = getFirstVex(i);
 80         //不等于-1说明是存在的
 81          while (firstVex!=-1) {
 82              //如果存在且没有被访问过就进行访问
 83              if (!isVisted[firstVex]) {
 84                  DFS(isVisted, firstVex);
 85              }
 86               firstVex = getNextVex(i, firstVex);
 87          }
 88     }
 89
 90     public void DFS(){
 91         for (int i = 0; i <arrayList.size(); i++) {
 92             if(!isVisted[i]){
 93                 //进行回溯
 94                 DFS(isVisted,i);
 95             }
 96         }
 97     }
 98     /**
 99      * 添加节点
100      * @param vex
101      */
102     public void InsertVex(String vex){
103         arrayList.add(vex);
104     }
105
106     /**
107      * 设置边
108      * @param v1 第一个节点对应的下标
109      * @param v2  第二节点对应的下标
110      * @param weight 两个节点对应的权值
111      */
112     public void InsertEdeges(int v1,int v2,int weight){
113         TwoArray[v1][v2]=weight;
114         TwoArray[v2][v1]=weight;
115         numOfEdges++;
116     }
117
118     /**
119      * 返回节点对应的个数
120      * @return
121      */
122     public int numVex(){
123         return arrayList.size();
124     }
125
126     /**
127      * 返回边的总个数
128      * @return
129      */
130     public int numEdges(){
131         return numOfEdges;
132     }
133
134     /**
135      * 显示邻接矩阵（图的展示）
136      */
137     public void Show(){
138         for (int[] ints : TwoArray) {
139             System.out.println(Arrays.toString(ints));
140         }
141     }
142
143     /**
144      * 根据下标获取对应的数据
145      * @param i 下标
146      * @return
147      */
148     public String getValue(int i){
149         return arrayList.get(i);
150     }
151
152     public int getWeight(int v1,int v2){
153         int weight=TwoArray[v1][v2];
154         return weight;
155     }
156 }

代码执行结果如下：