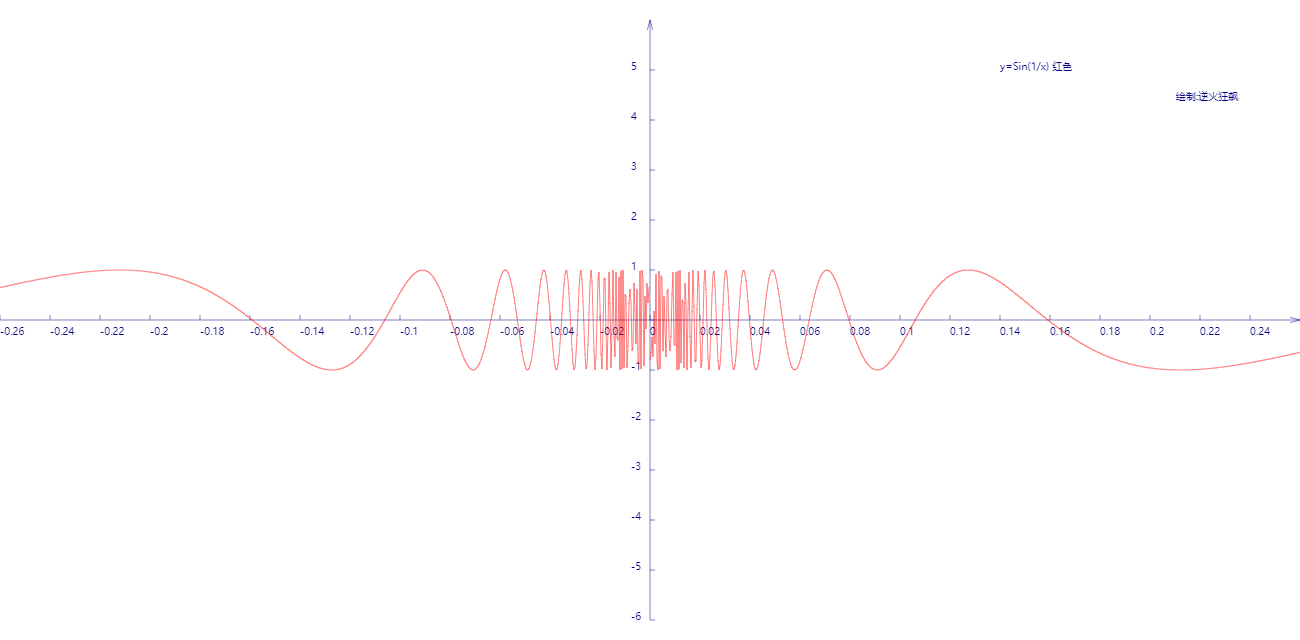
函数y=sin(1/x)曲线

该曲线在x趋近于零时振荡很剧烈，在远离零点时振荡越来越平缓。

图线：

代码：

<!DOCTYPE html>
<html lang="utf-8">
<meta http-equiv="Content-Type" content="text/html; charset=utf-8"/>
<head>
     <title>绘制曲线y=Sin(1/x)</title>
    </head>

     <body onload="draw()">
        <canvas id="myCanvus" width="1300px" height="640px" style="border:1px dashed black;">
            出现文字表示你的浏览器不支持HTML5
        </canvas>
     </body>
</html>
<script type="text/javascript">
<!--
    function draw(){
        var canvas=document.getElementById("myCanvus");
        var canvasWidth=1300;
        var canvasHeight=640;

        var context=canvas.getContext("2d");

        context.fillStyle = "white";
        context.fillRect(0, 0, canvasWidth, canvasHeight);

        context.strokeStyle = "black";
        context.fillStyle = "black";

        // 进行坐标变换：把原点放在左下角，东方为X轴正向，北方为Y轴正向
        var offsetY=320;// Y向偏移值，正值向上偏，用来画坐标轴
        var offsetX=650;// X向偏移值，正值向右偏，用来画坐标轴

        context.save();
        context.translate(0+offsetX,canvasHeight-offsetY);

        drawAxisXText(context);// 文字和线分开画比较好处理
        drawAxisYText(context);
        drawTitleText(context);

        context.rotate(getRad(180));
        context.scale(-1,1);        

        drawAxisX(context);
        drawAxisY(context);
        drawCurve(context);       

        context.restore();
    }

    function drawTitleText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var x=350;
        var y=-250;

        // 写文字
        ctx.fillText("y=Sin(1/x) 红色",x,y);
        //ctx.fillText("y=(x-4)^4-1 绿色",x,y+20);
        //ctx.fillText("y=(x+4)^4+5(x+4)^2-1 黄色",x,y+40);
        //ctx.fillText("y=(x-7)^5 青柠色",x,y+60);
        //ctx.fillText("y=(x+3)^0.5 紫色",x,y+80);
        //ctx.fillText("y=(x+5)^0.33 栗色",x,y+100);

        ctx.fillText("  绘制:逆火狂飙",x+170,y+30);
    }

    function drawCurve(ctx){
        var cds=[{}];
        var cds1=[{}];
        var cds2=[{}];
        var cds3=[{}];
        var cds4=[{}];
        var cds5=[{}];
        var cds6=[{}];

        var x,y,arr;
        for(x=-13;x<=13;x+=0.0004){
            if(x<0){
                y=Math.sin(1/x);// x<0
                arr={"x":x,"y":y};
                cds.push(arr);
            }

            if(x>0){
                y=Math.sin(1/x);// x<0
                arr={"x":x,"y":y};
                cds1.push(arr);
            }

        }

        paintCurve(ctx,"red",cds);
        paintCurve(ctx,"red",cds1);
    }

    function paintCurve(ctx,color,cds){
        var SU=50;// Scale Unit

        ctx.strokeStyle = color;
        ctx.beginPath();
        for(var i=0; i<cds.length; i++){
            ctx.lineTo(cds[i].x*SU*SU,cds[i].y*SU);// 注意y轴比例
        }
        ctx.stroke();
        ctx.closePath();
    }

    function drawAxisX(ctx){
        ctx.save();

        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-650;
        var end=650;

        // 画轴
        ctx.beginPath();
        ctx.moveTo(start, 0);
        ctx.lineTo(end, 0);
        ctx.stroke();
        ctx.closePath();

        // 画箭头
        ctx.beginPath();
        ctx.moveTo(end-Math.cos(getRad(15))*10, Math.sin(getRad(15))*10);
        ctx.lineTo(end, 0);
        ctx.lineTo(end-Math.cos(getRad(15))*10, -Math.sin(getRad(15))*10);
        ctx.stroke();
        ctx.closePath();

        // 画刻度
        var x,y;
        y=5;
        for(x=start;x<end;x+=50){
            ctx.beginPath();
            ctx.moveTo(x, 0);
            ctx.lineTo(x, y);

            ctx.stroke();
            ctx.closePath();
        }

        ctx.restore();
    }

    function drawAxisXText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-650;
        var end=650;

        // 写文字
        var x,y=5;
        for(x=start;x<end;x+=50){
            ctx.fillText(x/50/50,x,y+10);
        }
    }

    function drawAxisY(ctx){
        ctx.save();

        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-300;
        var end=300;

        // 画轴
        ctx.beginPath();
        ctx.moveTo(0, start);
        ctx.lineTo(0, end);
        ctx.stroke();
        ctx.closePath();

        // 画箭头
        ctx.beginPath();
        ctx.moveTo(Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
        ctx.lineTo(0, end);
        ctx.lineTo(-Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
        ctx.stroke();
        ctx.closePath();

        // 画刻度
        var x,y;
        x=5;
        for(y=start;y<end;y+=50){// 注意y轴比例
            ctx.beginPath();
            ctx.moveTo(x, y);
            ctx.lineTo(0, y);

            ctx.stroke();
            ctx.closePath();
        }
    }

    function drawAxisYText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-250;
        var end=350;

        // 写文字
        var x=-19,y=5;
        for(y=start;y<end;y+=50){

            if(y!=0){
                ctx.fillText(-y/50,x,y);// 注意y轴比例
            }
        }
    }

    function getRad(degree){
        return degree/180*Math.PI;
    }

    function cutShort(str,length){
        if(str.length>length){
            str=str.substr(0,length)+"...";
        }

        return str;
    }
//-->
</script>

函数y=sin(1/x)曲线的更多相关文章

由函数$y=\sin x$的图像伸缩变换为函数$y=\sin(\omega x)$的图像(交互式)
可以拖动滑动条$\omega$显示动态效果
绘制函数 y=x^2-2x-3/2x^2+2x+1 的曲线
代码: <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Type ...
在笛卡尔坐标系上描绘函数 y=4x^2-2/4x-3
代码: <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Type ...
[再寄小读者之数学篇](2014-11-19 $\sin(x+y)=\sin x\cos y+\cos x\sin y$)
$$\bex \sin(x+y)=\sin x\cos y+\cos x\sin y. \eex$$ Ref. [Proof Without Words: Sine Sum Identity, The ...
使用神经网络来拟合函数y = x^3 +b
我们使用一个三层的小网络来,模拟函数y = x^3+b函数 import tensorflow as tf import numpy as np import matplotlib.pyplot as ...
PSO：利用PSO+ω参数实现对一元函数y = sin(10*pi*x) ./ x进行求解优化，找到最优个体适应度—Jason niu
x = 1:0.01:2; y = sin(10*pi*x) ./ x; figure plot(x, y) title('绘制目标函数曲线图—Jason niu'); hold on c1 = 1. ...
PSO：利用PSO实现对一元函数y = sin(10*pi*x) ./ x进行求解优化，找到最优个体适应度—Jason niu
x = 1:0.01:2; y = sin(10*pi*x) ./ x; figure plot(x, y) title('绘制目标函数曲线图—Jason niu'); hold on c1 = 1. ...
函数 y=x^x的分析
关于函数 y=xx的分析: 由图像得,y在负无穷大到0图像处处不连续,故y的定义域为(0,正无穷大): 故该函数不就是y=e^(lnxx)吗? 1.定义域:我们变形一下,y=e^(xlnx),显然是0 ...
2、函数y=f(x)
/* Note:Your choice is C IDE */ #include "stdio.h" /* 3.函数y=f(x)可表示为: */ void main() { int ...

随机推荐

poj2485(Kruskal)
这道题显然是一道最小生成树的问题,参考算法导论中的Kruskal方法,先对路径长度进行排序,然后使用并查集(Disjoint Set Union)来判断节点是否连通,记录连接所有节点的最后一条路径的长 ...
python 爬虫 User-Agent
USER_AGENTS = [ "Mozilla/5.0 (Windows NT 6.1; WOW64) AppleWebKit/537.1 (KHTML, like Gecko) Chro ...
解释Crypto模块怎么就这么"皮"？No module named "Crypto"
https://www.cnblogs.com/fawaikuangtu123/p/9761943.html python版本:python3.6,系统:win7 1.pip install cryp ...
FastReport.Net使用：[37]报表继承
1.设计一个基础报表,将其保存为BaseReport. 2.新建一个继承的报表. 通过文件-->新建打开“新建对象”向导.选择“继承的报表”,点击确定. 3. 在打开对话框中选择基础报表Ba ...
51Nod1962 区间计数
这题与之前那道区间最值的题非常类似,依旧是二分区间,然后统计跨过中间点的区间贡献. 我们要选出小于等于和小于的,这样就可以算出相等的区间长了. 复杂度O(nlogn) By:大奕哥 #include& ...
Android Studio --> Gradle Build设置自动
ps:http://www.cnblogs.com/kangyi/p/4448398.html 应用场景通常情况下我们的apps发布后也就是release模式下log是不显示的,debug模式下是显 ...
bzoj 3289 莫队逆序对
莫队维护逆序对,区间左右增减要分类讨论. 记得离散化. /************************************************************** Problem: ...
[转]Android适配器之ArrayAdapter、SimpleAdapter和BaseAdapter的简单用法与有用代码片段
收藏ArrayAdapter.SimpleAdapter和BaseAdapter的一些简短代码片段,希望用时方便想起其用法. 1.ArrayAdapter 只可以简单的显示一行文本代码片段: A ...
PHP简单利用 token 防止表单重复提交
<?php /* * 隐藏一个可变的token,每次提交都需要和服务器校对 */ session_start(); function set_token() { $_SESSION['token ...
关于图表第三方Charts的一些理解与总结
最近项目中用到了很多的图表,如柱状图,线状图,饼状图等等.接触到了一个新的第三方Charts,在做图方面确实非常强大,在使用了一段时间后,今天对他进行一个小的总结,也是自己的一点小理解. 关于char ...

函数y=sin(1/x)曲线

函数y=sin(1/x)曲线的更多相关文章

随机推荐

热门专题