poj3585 Accumulation Degree【树形DP】【最大流】

Accumulation Degree

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions:3151		Accepted: 783

Description

Trees are an important component of the natural landscape because of their prevention of erosion and the provision of a specific ather-sheltered ecosystem in and under their foliage. Trees have also been found to play an important role in producing oxygen and reducing carbon dioxide in the atmosphere, as well as moderating ground temperatures. They are also significant elements in landscaping and agriculture, both for their aesthetic appeal and their orchard crops (such as apples). Wood from trees is a common building material.

Trees also play an intimate role in many of the world's mythologies. Many scholars are interested in finding peculiar properties about trees, such as the center of a tree, tree counting, tree coloring. A(x) is one of such properties.

A(x) (accumulation degree of node x) is defined as follows:

1. Each edge of the tree has an positive capacity.
2. The nodes with degree of one in the tree are named terminals.
3. The flow of each edge can't exceed its capacity.
4. A(x) is the maximal flow that node x can flow to other terminal nodes.

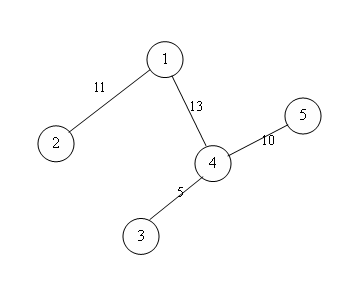
Since it may be hard to understand the definition, an example is showed below:

A(1)=11+5+8=24
Details:	1->2	11
	1->4->3	5
	1->4->5	8(since 1->4 has capacity of 13)
A(2)=5+6=11
Details:	2->1->4->3	5
	2->1->4->5	6
A(3)=5
Details:	3->4->5	5
A(4)=11+5+10=26
Details:	4->1->2	11
	4->3	5
	4->5	10
A(5)=10
Details:	5->4->1->2	10

The accumulation degree of a tree is the maximal accumulation degree among its nodes. Here your task is to find the accumulation degree of the given trees.

Input

The first line of the input is an integer T which indicates the number of test cases. The first line of each test case is a positive integer n. Each of the following n - 1 lines contains three integers x, y, z separated by spaces, representing there is an edge between node x and node y, and the capacity of the edge is z. Nodes are numbered from 1 to n.
All the elements are nonnegative integers no more than 200000. You may assume that the test data are all tree metrics.

Output

For each test case, output the result on a single line. 
　

Sample Input

1
5
1 2 11
1 4 13
3 4 5
4 5 10

Sample Output

26

Source

South Central China 2008 hosted by NUDT

题意：

给定一棵不定根的树。水流从根流出（源点），流向叶子节点（汇点），每条边有一个容量。整个水系的流量定义为源点流出的水量。求哪个点作为源点时，整个水洗的流量最大，输出这个最大值。

思路：

用d[x]表示以x为根的子树中，把x作为源点，从x出发流向子树的流量最大值。比较暴力的方法是枚举源点，每次都计算他的流量。时间时O(n^2)显然不行。

下面介绍一种“二次扫描与换根法”

代替源点的枚举，就可以在O(N)时间内解决整个问题。

首先任选一个点root，求出以他为根是的d数组。

设f[x]表示把x作为源点，流向整个水系，流量的最大值。显然 f[root] = d[root]

当f[x]被求出时，考虑他的子节点y，f[y]包含两部分：1.从y流向以y为根的子树的流量，即d[y]中的值。 2.从y沿着父节点x的河道，进而流向水系中其他部分的流量。

x作为源点的总流量为f[x]， 从x流向y的流量为min(d[y], c(x,y)),所以从x流向除y以外其他部分的流量就是二者之差。再与c(x,y)取最小值就可以得到以y作为源点，先流到x在流向其他部分的流量。那么得到f[y]就是把源点从x换成y之后，流量的计算结果。

 //#include <bits/stdc++.h>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<stdio.h>
 #include<cstring>
 #include<vector>
 #include<map>

 #define inf 0x3f3f3f3f
 using namespace std;
 typedef long long LL;

 int n;
 const int maxn = 2e5 + ;
 int head[maxn], cnt = , d[maxn], deg[maxn], f[maxn];
 struct edge{
     int x, y;
     int nxt;
     int c;
 }edge[maxn * ];

 void init()
 {
     memset(head, -, sizeof(head));
     cnt = ;
     memset(d, , sizeof(d));
     memset(deg, , sizeof(deg));
 }

 void addedge(int x, int y, int w)
 {
     edge[cnt].x = x;
     edge[cnt].y = y;
     edge[cnt].c = w;
     edge[cnt].nxt = head[x];
     head[x] = cnt++;
     edge[cnt].x = y;
     edge[cnt].y = x;
     edge[cnt].c = w;
     edge[cnt].nxt = head[y];
     head[y] = cnt++;
     deg[x]++;
     deg[y]++;
 }

 void dfs(int rt, int fa)
 {
     int ans = ;
     for(int i = head[rt]; i != -; i = edge[i].nxt){
         int y = edge[i].y;
         if(y == fa){
             continue;
         }
         if(deg[y] == ){
             ans += edge[i].c;
         }
         else{
             dfs(y, rt);
             ans += min(d[y], edge[i].c);
         }
     }
     d[rt] = ans;
     return ;
 }

 void dp(int x, int fa)
 {
     for(int i = head[x]; i != -; i = edge[i].nxt){
         int y = edge[i].y;
         if(edge[i].y == fa)continue;
         if(deg[x] == ){
             f[y] = d[y] + edge[i].c;
         }
         else{
             f[y] = d[y] + min(f[x] - min(d[y], edge[i].c), edge[i].c);
         }
         dp(y, x);
     }
 }

 int main()
 {
     int t;
     scanf("%d", &t);
     while(t--){
         init();
         scanf("%d", &n);
         for(int i = ; i < n - ; i++){
             int x, y, w;
             scanf("%d%d%d", &x, &y, &w);
             addedge(x, y, w);
         }

         int s = ;
         dfs(s, );
         f[s] = d[s];
         dp(s, );
         int ans = ;
         for(int i = ; i <= n; i++){
             ans = max(ans, f[i]);
         }
         printf("%d\n", ans);

     }
     return ;
 }