ACM-Antiprime数
问题描述: swust打不开,随便找了个博客。。。。
对于任何正整数x,起约数的个数记做g(x).例如g(1)=1,g(6)=4.
定义:如果某个正整数x满足:对于任意i(0<i<x),都有g(i)<g(x),则称x为反素数.
现在给一个N,求出不超过N的最大的反素数.
比如:输入1000 输出 840
思维过程:
求[1..N]中最大的反素数-->求约数最多的数(约数同样多取数值小的)
简单证明:
如果X是答案,但X不是约数最多的数,假设约数最多的数是Y,那么Y>X,否则不符合反质数的定义。
那么很明显Y也是一个反质数,且Y比X大,那么答案应该是Y而不是X。
如果求约数的个数 756=2^2*3^3*7^1
(2+1)*(3+1)*(1+1)=24
基于上述结论,给出算法:按照质因数大小递增顺序搜索每一个质因子,枚举每一个质因子
为了剪枝:
性质一:一个反素数的质因子必然是从2开始连续的质数.
因为最多只需要10个素数构造:2,3,5,7,11,13,17,19,23,29
性质二:p=2^t1*3^t2*5^t3*7^t4.....必然t1>=t2>=t3>=....
//// Antiprime数.cpp : 定义控制台应用程序的入口点。
////
//
#include "stdafx.h" #include<cstdio>
#include<iostream>
using namespace std;
typedef long long ll;
int prime[] = { , , , , , , , , , , };
//相应的限制次数{ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11};
//2*3*5*7*11*13*17*19*21*23>n,所以只需考虑到23即可
ll n, BestSum, BestNum; //num表示当前数字大小、sum表示当前数字的约数个数、limit表示第k个素数的上限,k表示第k个素数
void solve(ll num, ll sum, ll limit, ll k)
{
//cout << "=======================: pos:" << k << "\tdiv:" << sum << "\tnum:" << num << "\tlimit:" << limit << endl;
if (sum>BestSum){
BestSum = sum;
BestNum = num;
}
else if (sum == BestSum&&num<BestNum){//约数个数一样时,取小数
BestNum = num;
}
for (int i = ; i <= limit; i++){//素数k取i个
cout << "=====================================================================" << endl;
cout << "now num:" << num << "\tk:" << k << "\ti:" << i << "\tlimit:" << limit << endl;
cout << num << "*prime[" << k << "]=" << "="<<num <<"*"<<prime[k]<< "=" << num * prime[k] << endl;
cout << "sum:" << sum << "\ti:" << i << "\tsum*(1+" << i << ")=" << sum*( + i) << endl;
cout << "=====================================================================" << endl<<endl;
num *= prime[k];
if (num>n) return;
solve(num, sum*( + i), i, k + );
}
}
int main(){
cin >> n;
solve(, , , );//每个数最多被分解成10质数的乘积
cout << BestNum;
return ;
}
下面是当n=20时,问题解的遍历图形。
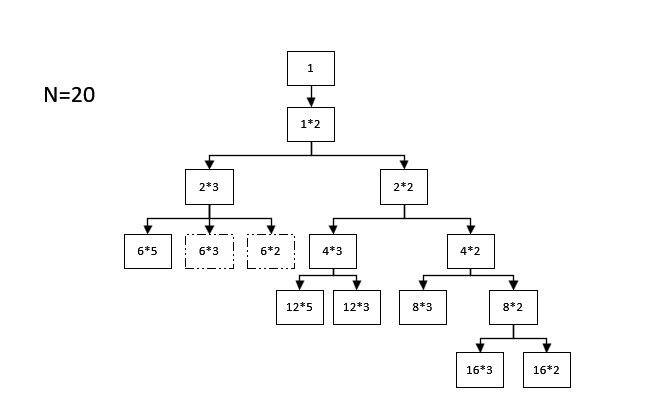
ACM-Antiprime数的更多相关文章
- [swustoj 373] Antiprime数
Antiprime数(0373) 问题描述 如果一个自然数n(n>=1),满足所有小于n的自然数(>=1)的约数个数都小于n的约数个数,则n是一个Antiprime数.譬如:1, 2, 4 ...
- COGS 693. [SDOI2005]Antiprime数 唯一分解定理逆用
693. Antiprime数 ★★ 输入文件:antip.in 输出文件:antip.out 简单对比 时间限制:1 s 内存限制:128 MB 如果一个自然数n(n>=1), ...
- Antiprime数-数论
题目描述 Description 如果一个自然数n满足:所有小于它的自然数的约数个数都小于n的约数个数,则称n是一个Antiprime数.譬如:1.2.4.5.12.24都是Antiprime数. ...
- 巴蜀1088 Antiprime数
Description 如果一个自然数n(n>=1),满足所有小于n的自然数(>=1)的约数个数都小于n的约数个数,则n是一个Antiprime数.譬如:1, 2, 4, 6, 12, 2 ...
- ACM 删数问题 SDUT 2072
http://acm.sdut.edu.cn/onlinejudge2/index.php/Home/Index/problemdetail/pid/2072.html 删数问题 Time Limit ...
- ACM——完数
完数 时间限制(普通/Java):1000MS/3000MS 运行内存限制:65536KByte 总提交:1930 测试通过:413 描述 自然数中,完数寥若晨 ...
- 南阳acm奇偶数分离
这道题的特殊要求是要先先限定了测试数据的组数,所以多加一条循环语句.下面是已通过的代码: #include<stdio.h> main() { int n,m,i,j; ...
- ACM 阶乘数位数
描述 N!阶乘是一个非常大的数,大家都知道计算公式是N!=N*(N-1)······*2*1.现在你的任务是计算出N!的位数有多少(十进制)? 输入 首行输入n,表示有多少组测试数据(n<1 ...
- ACM Fibonacci数 计算
Fibonacci数 时间限制:3000 ms | 内存限制:65535 KB 难度:1 描述 无穷数列1,1,2,3,5,8,13,21,34,55...称为Fibonacci数列,它可以递 ...
- ACM题目————数素数
令Pi表示第i个素数.现任给两个正整数M <= N <= 104,请输出PM到PN的所有素数. 输入格式: 输入在一行中给出M和N,其间以空格分隔. 输出格式: 输出从PM到PN的所有素数 ...
随机推荐
- Session共享解决方案
使用nginx做的负载均衡添加一个ip_hash配置 一.开两个Tomcat写测试程序 @WebServlet("/nginxSessionServlet") public cla ...
- FineReport帆软报表需求:根据url传递过来的参数值决定显示隐藏列
需求:角色id传递到报表页面中,然后根据角色id,决定隐藏第1列,显示第2-4列,还是隐藏第2-4列,显示第1列. 解决方法:
- JS事件委托或者事件代理原理以及实现
事件委托(事件代理)原理:简单的说就是将事件交由别人来执行,就是将子元素的事件通过冒泡的形式交由父元素来执行. 为什么要用时间委托? 在JavaScript中,添加到页面上的事件处理程序数量将直接关系 ...
- C++11常用特性介绍——auto类型修饰符
1.C++11常用特性介绍 从本篇开始介绍C++11常用特性,大致分:关键字及新语法.STL容器.多线程.智能指针内存管理,最后讲一下std::bind和std::function 二.关键字和新语法 ...
- Linux centos VMware Nginx防盗链、Nginx访问控制、Nginx解析php相关配置、Nginx代理
一.Nginx防盗链 配置如下,可以和上面的配置结合起来 location ~* ^.+\.(gif|jpg|png|swf|flv|rar|zip|doc|pdf|gz|bz2|jpeg|bmp|x ...
- matlab练习程序(龙格库塔法)
非刚性常微分方程的数值解法通常会用四阶龙格库塔算法,其matlab函数对应ode45. 对于dy/dx = f(x,y),y(0)=y0. 其四阶龙格库塔公式如下: 对于通常计算,四阶已经够用,四阶以 ...
- Using SmartAssembly with MSBuild
SmartAssembly 6 SmartAssembly 6 documentation Building your assembly Using SmartAssembly with MSBuil ...
- 吴裕雄 Bootstrap 前端框架开发——Bootstrap 辅助类:元素浮动到右边
<!DOCTYPE html> <html> <head> <meta charset="utf-8"> <title> ...
- 【转载】Oracle创建数据库和用户
以前开发的时候用得比较多的是mysql和sql server,oracle用的比较少,用起来比较生疏,mysql和sql server用起来比较类似,就oracle的使用方式和他们不同,oracle在 ...
- Vue二次精度随笔(2)
1.vue中数组更新是否会引起视图刷新的研究 (1)vue中修改数组可以引起视图刷新的方法 (2)不会引起数组刷新的方法,需要手动进行赋值 (3)有些数组的变化是不能够引起视图的刷新的,一个是修改数组 ...
