POJ3352 Road Construction Tarjan+边双连通

题目链接：http://poj.org/problem?id=3352

题目要求求出无向图中最少需要多少边能够使得该图边双连通。

在图G中，如果任意两个点之间有两条边不重复的路径，称为“边双连通”，去掉任何一条边都是其他边仍然是连通的，也就是说边双连通图中没有割边。

算法设计是：运用tarjan+缩点。对于每一个边双连通分量，我们都可以把它视作一个点，因为low值相同的点处在同一个边双连通分量中，可以简单地思考一下，（u,v）之间有两条可达的路径，dfs一定可以从一条路开始搜索并且从另一条路回去。而边双连通分量最初开始搜索的一个点的编号就是这个边双连通分量的low值，因为假设这个点的low值更加靠前的话，他与之前的结点一定是边双连通的关系，有一条边搜索到这个点，这个点在之后还有一条不重合的路径能到达先前那个结点，与边双连通分量的最大性产生矛盾，其实我们也可以把那个点收纳进这个边连通分量，把它作为该连通分量第一个进入dfs树的结点。故有边双连通分量中的点low值相同。

最终将这些点变成一个新的点图，这个点图中最大的边双连通分量就是一个点，所以我们只要看在这张图中需要加多少条边可以使得它边双连通就行。可以证明使得缩点图边双连通加上的边数是 （1+度数为1的点的数量）/2。由于这些缩点的low值都是不同的，所以我们可以用low值作为degree（点的度数）的索引。计算度数的时候时候扫描所有的点，只要跟一个low值不同的点有边，那么该low值（缩点）一定有一个外界的度（可看成入度），最后统计最终的只有一个度的连通分量数量即可。

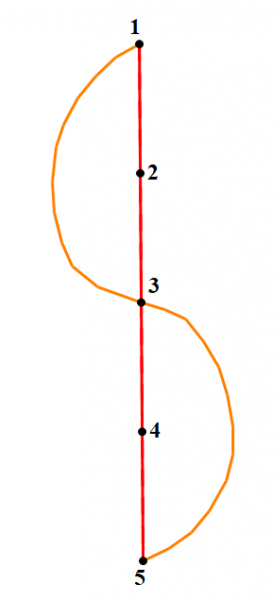
用下面这张图同样可以证明为什么边双连通分量中的dfs中更新low值为什么是代码中所说的那样一个过程，因为low[3]是等于1的，而3的dfs顺序，就是dfn[3]=3,到了五号结点的时候，我们发现有回退边（5,3）如果此时我们用3的dfn值来更新5的low值的话就会发现5的low是3，回溯之后发现1,2,3结点low值是1，而4,5结点的low值是3，这样真的正确吗？很遗憾是错误的，为什么呢？我们可以发现，是因为在五号结点访问边（5,3）的时候错过了3号节点的回退边（3,1）在边双连通分量的计算中，回退边是需要包括在内的，这样dfs搜索到这个点之后这个点可以通过多条回退边跳回一个low=dfn结点，这个结点的low值就是他要更新成为的值。故边双连通分量中low的计算可以说是十分简洁但是要区分开和其他tarjan算法的low值计算策略，主要tarjan的这个low值太牛逼了！！！包含了太多的信息orz

代码如下：

 #include<cstring>
 #include<vector>
 #include<stdio.h>
 using namespace std;
 const int maxn =;
 int n,m,low[maxn],dfn;
 vector<int>G[maxn];
 void dfs(int u,int fa)//先用dfs处理处每个点的low值，以便相同的low值合并
 {//处理low值时不需要处理dfn数组
     low[u]=++dfn;
     for(int i=;i<G[u].size();i++)
     {
         int v=G[u][i];
         if(v==fa)continue;//保证dfs 树的前向性
         if(!low[v])
             dfs(v,u);
             low[u]=min(low[u],low[v]);
      }
 }
 int tarjan()
 {
     int degree[maxn];
     memset(degree,,sizeof(degree));
     for(int i=;i<=n;i++)
     {
         for(int j=;j<G[i].size();j++)
         {
             if(low[i]!=low[G[i][j]])
                 degree[low[i]]++;
         }
     }
     int res=;
     for(int i=;i<=n;i++)
     {
         if(degree[i]==)res++;
     }
     return res;
 }
 int main()
 {
     while(~scanf("%d%d",&n,&m))
     {
         int x,y;
         memset(low,,sizeof(low));
         for(int i=;i<=n;i++)G[i].clear();
         while(m--)
         {
             scanf("%d%d",&x,&y);
             G[x].push_back(y);
             G[y].push_back(x);
         }
         dfn=;//每次dfs之前设置dfs树的编号从1开始
         dfs(,-);
         int ans=tarjan();
         printf("%d\n",(ans+)/);
     }
     return ;
  }