SVM多核学习方法简介

作者：Walker

SVM是机器学习有监督学习的一种方法，常用于解决分类问题，其基本原理是：在特征空间里寻找一个超平面，以最小的错分率把正负样本分开。因为SVM既能达到工业界的要求，机器学习研究者又能知道其背后的原理，所以SVM有着举足轻重的地位。

但是我们之前接触过的SVM都是单核的，即它是基于单个特征空间的。在实际应用中往往需要根据我们的经验来选择不同的核函数（如：高斯核函数、多项式核函数等）、指定不同的参数，这样不仅不方便而且当数据集的特征是异构时，效果也没有那么好。正是基于SVM单核学习存在的上述问题，同时利用多个核函数进行映射的多核学习模型（MKL）应用而生。

多核模型比单个核函数具有更高的灵活性。在多核映射的背景下，高维空间成为由多个特征空间组合而成的组合空间。由于组合空间充分发挥了各个基本核的不同特征映射能力，能够将异构数据的不同特征分量分别通过相应的核函数得到解决。目前主流的多核学习方法主要包括合成核方法、多尺度核方法和无限核方法。其具体流程如图1所示：

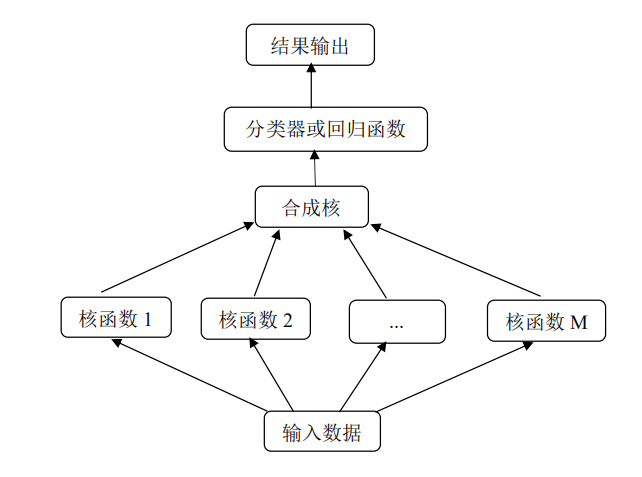
图1 多核学习流程图

接下来我们以二分类问题为例，为大家简单介绍多核学习方法。令训练数据集为X={(x₁,y₁),(x₂,y₂),(x₃,y₃)…(x_n,y_n)}，其中X_i是输入特征，且X_i∈R^d，i= 1,2, …, N，Y_i∈{+1, −1}是类标签。SVM 算法目标在于最大化间隔，其模型的原始问题可以表示为：

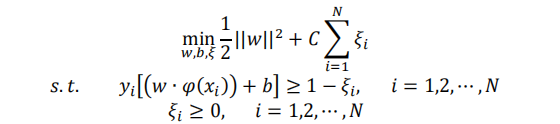
其中，w是待求的权重向量，ζ_i与C分别是松弛变量和惩罚系数。根据拉格朗日对偶性以及 KKT 条件，引入核函数K( X_i , X_j): Rn×Rn → R，原始问题也可以转换成如下最优化的形式：

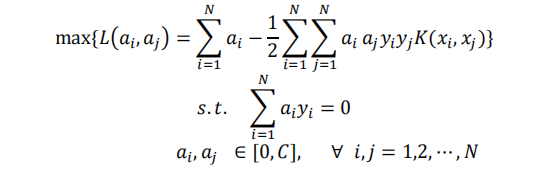
其中，ai与aj为拉格朗日乘子，核函数K( Xi, Xj)=φ(xi) xφ(xj)。核方法的思想就是，在学习与预测中不显示地定义映射函数φ(xi) ，只定义核函数K( Xi, Xj)，直接在原低维空间中计算高维空间中的向量内积，既实现低维样本空间到高维特征空间的映射，又不增加计算复杂量。

多核学习方法是单核 SVM 的拓展，其目标是确定 M 个个核函数的最优组合，使得间距最大，可以用如下优化问题表示：

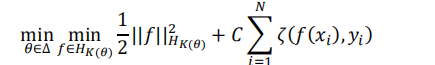
其中∆= {θ∈ ℝ+|θ^Te_M=1},表示 M 个核函数的凸组合的系数，e_M是一个向量，M个元素全是 1，K(θ)=∑^M_j=1θ_jk_j(∙,∙)代表最终的核函数，其中k_j(∙,∙)是第j个核函数。与单核 SVM 一样，可以将上式如下转化：

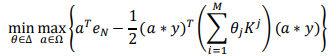
其中K^j∈ R^NxN,Ω={a|a∈[0,C]^N},“∗”被定义为向量的点积，即(1,0)∗(2,3) = (1 ×2 ,0×3)=(2,0)。通过对比 MKL 与单核 SVM 所对应的优化问题形式，求解多核学习问题的计算复杂度与难度会远大于单核 SVM，所以研究出一种高效且稳定的算法来解决传统多核学习中的优化难题，仍然很具有挑战性。

综上所示，尽管多核学习在解决一些异构数据集问题上表现出了非常优秀的性能，但不得不说效率是多核学习发展的最大瓶颈。首先，空间方面，多核学习算法由于需要计算各个核矩阵对应的核组合系数，需要多个核矩阵共同参加运算。也就是说，多个核矩阵需要同时存储在内存中，如果样本的个数过多，那么核矩阵的维数也会非常大，如果核的个数也很多，这无疑会占用很大的内存空间。其次，时间方面，传统的求解核组合参数的方法即是转化为SDP优化问题求解，而求解SDP问题需要使用内点法，非常耗费时间，尽管后续的一些改进算法能在耗费的时间上有所减少，但依然不能有效的降低时间复杂度。高耗的时间和空间复杂度是导致多核学习算法不能广泛应用的一个重要原因。

下篇预告：不同核学习方法的研究。

参考文献：Research on Multiple Kernel Boosting Learning Algorithm

Fast Multiple Kernel Learning for Classification and Application

Research on Multiple Kernel Learning Algorithms and Their Applications