poj 3013 最短路SPFA算法

POJ_3013_最短路

Big Christmas Tree

Time Limit: 3000MS		Memory Limit: 131072K
Total Submissions: 23630		Accepted: 5125

Description

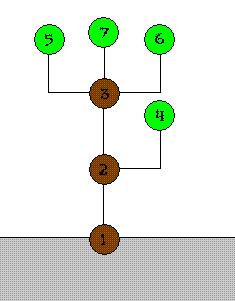Christmas is coming to KCM city. Suby the loyal civilian in KCM city is preparing a big neat Christmas tree. The simple structure of the tree is shown in right picture.

The tree can be represented as a collection of numbered nodes and some edges. The nodes are numbered 1 through n. The root is always numbered 1. Every node in the tree has its weight. The weights can be different from each other. Also the shape of every available edge between two nodes is different, so the unit price of each edge is different. Because of a technical difficulty, price of an edge will be (sum of weights of all descendant nodes) × (unit price of the edge).

Suby wants to minimize the cost of whole tree among all possible choices. Also he wants to use all nodes because he wants a large tree. So he decided to ask you for helping solve this task by find the minimum cost.

Input

The input consists of T test cases. The number of test cases T is given in the first line of the input file. Each test case consists of several lines. Two numbers v, e (0 ≤ v, e ≤ 50000) are given in the first line of each test case. On the next line, v positive integers w_i indicating the weights of v nodes are given in one line. On the following e lines, each line contain three positive integers a, b, c indicating the edge which is able to connect two nodes a and b, and unit price c.

All numbers in input are less than 2¹⁶.

Output

For each test case, output an integer indicating the minimum possible cost for the tree in one line. If there is no way to build a Christmas tree, print “No Answer” in one line.

Sample Input

2
2 1
1 1
1 2 15
7 7
200 10 20 30 40 50 60
1 2 1
2 3 3
2 4 2
3 5 4
3 7 2
3 6 3
1 5 9

Sample Output

15
1210

题意：给一张点和边都有权的图，现在要求其一棵以1结点为根的生成树使树的边权和最小，树边权 = 对应的图边权 * 树边末端点为根的子树所有结点对于图顶点的点权和。
思路：要求∑(边权*子树点权和)，等价于求∑(点权*点到根路径上的边权和)。
　　由于所要求的花费最小，所以这是个最短路问题。因为跟节点为1，求1到各个点的最小值，每个点的权值乘所经过的边加起来就好了

样例中的计算方法
40*(4+3+1)+60*(2+3+1)+50*(3+3+1)+20*(3+1)+10*1+30*(2+1)=

记得要最短路，所以样例中的1  5  9放弃。
　　根据数据，需要SPFA优化。SPFA优化了B-F算法的很多无效操作，只对发生更新的点进行操作。
　　存图时我采用了链式前向星，它是反着来的，当然vector也行，不过据说很慢。　　关于链式前向星，这个博客讲的非常好：地址。。具体的我也不太愿意写了，因为内容基本相似。
　　Bellman-Ford有很多低效或无效的操作，其核心部分在于每一轮操作更新所有节点到起点s的最短距离。因此，在计算节点u之后，下一步只计算和调整它的邻居，可以加快收敛速度。
queue就是这么个操作。记得while一轮后，vis[u]=0,否则会wa，因为u可能会重新入队。
　　

#include<iostream>
#include<cstring>
#include<queue>
typedef long long ll;
using namespace std;
const int maxn=;
#define inf (1ll<<60)
ll cnte=;
ll head[maxn];
ll verw[maxn];
bool vis[maxn];
ll v,e;
ll dis[maxn];
struct node
{
    int v,next;
    ll w;
}edge[maxn*];
void add(int a,int b,int w)　　//add操作
{
    edge[cnte].v=b;
    edge[cnte].w=w;
    edge[cnte].next=head[a];
    head[a]=cnte++;
}
bool spfa()
{
    for(int i=;i<=v;i++)
    {
        dis[i]=inf;
        vis[i]=false;
    }
    dis[]=;
    vis[]=;
    queue<int>q;
    q.push();
    while(!q.empty())
    {
        ll u=q.front();
        q.pop();　　
        for(int i=head[u];i!=-;i=edge[i].next)　　//遍历操作
        {
            ll v=edge[i].v;
            if(dis[v]>dis[u]+edge[i].w)
            {
                dis[v]=dis[u]+edge[i].w;

                if(!vis[v]){
                    q.push(v);
                    vis[v]=;
                }
            }
        }
        vis[u]=;　　//注意
    }
    for(int i=;i<=v;i++)
    {
        if(dis[i]==inf)
            return ;
    }
    return ;
}
int main()
{
    ll t;
    scanf("%lld",&t);
    while(t--)
    {
        scanf("%lld%lld",&v,&e);
        cnte=;
        for(int i=;i<=v;i++)
            scanf("%lld",&verw[i]);
        memset(head,-,sizeof(head));
        for(int i=;i<e;i++)
        {
            ll a,b,w;
            scanf("%lld%lld%lld",&a,&b,&w);
            add(a,b,w);
            add(b,a,w);
        }
        if(spfa())
            printf("No Answer\n");
        else
        {
            ll sum=;
            for(int i=;i<=v;i++)
            {
                sum+=verw[i]*dis[i];
            //    cout<<verw[i]<<" "<<dis[i]<<endl;
            }
            printf("%lld\n",sum);
        }
    }
}