Poj 3013基础最短路

Description

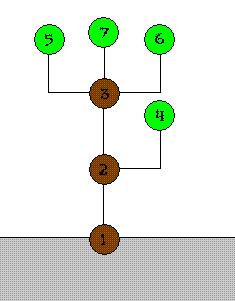Christmas is coming to KCM city. Suby the loyal civilian in KCM city is preparing a big neat Christmas tree. The simple structure of the tree is shown in right picture.

The tree can be represented as a collection of numbered nodes and some edges. The nodes are numbered 1 through n. The root is always numbered 1. Every node in the tree has its weight. The weights can be different from each other. Also the shape of every available edge between two nodes is different, so the unit price of each edge is different. Because of a technical difficulty, price of an edge will be (sum of weights of all descendant nodes) × (unit price of the edge).

Suby wants to minimize the cost of whole tree among all possible choices. Also he wants to use all nodes because he wants a large tree. So he decided to ask you for helping solve this task by find the minimum cost.

Input

The input consists of T test cases. The number of test cases T is given in the first line of the input file. Each test case consists of several lines. Two numbers v, e (0 ≤ v, e ≤ 50000) are given in the first line of each test case. On the next line, v positive integers w_i indicating the weights of v nodes are given in one line. On the following e lines, each line contain three positive integers a, b, c indicating the edge which is able to connect two nodes a and b, and unit price c.

All numbers in input are less than 2¹⁶.

Output

For each test case, output an integer indicating the minimum possible cost for the tree in one line. If there is no way to build a Christmas tree, print “No Answer” in one line.

Sample Input

2
2 1
1 1
1 2 15
7 7
200 10 20 30 40 50 60
1 2 1
2 3 3
2 4 2
3 5 4
3 7 2
3 6 3
1 5 9

Sample Output

15
1210

//INF开小会WA 开成0x3f3f3f3f  会WA

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N=;
const int M=;
int n,m,head[N],tot;
const long long INF=;
unsigned long long val[N],d[N];
bool vis[N];
struct node{
    int next,v,w;
}e[M];
void add(int u,int v,int w){
    e[tot].v=v;
    e[tot].next=head[u];
    e[tot].w=w;
    head[u]=tot++;
}
void spfa(){
    for(int i=;i<=n;++i) d[i]=INF,vis[i]=;
    queue<int>Q;
    Q.push();
    d[]=,vis[]=;
    while(!Q.empty()){
        int u=Q.front();
        Q.pop();
        vis[u]=;
        for(int i=head[u];i+;i=e[i].next){
            int v=e[i].v;
            if(d[v]>d[u]+e[i].w){
                d[v]=d[u]+e[i].w;
                if(!vis[v]) {
                    Q.push(v);vis[v]=;
                }
            }
        }
    }
    for(int i=;i<=n;++i) if(d[i]==INF) {puts("No Answer");return;}
    unsigned long long ans=;
    for(int i=;i<=n;++i)
        ans+=(long long)d[i]*val[i];
    printf("%llu\n",ans);
}
int main(){
    int T,u,v,x;
    for(scanf("%d",&T);T--;){
        scanf("%d%d",&n,&m);
        for(int i=;i<=n;++i) head[i]=-;
        tot=;
        for(int i=;i<=n;++i) scanf("%llu",&val[i]);
        while(m--){
        scanf("%d%d%d",&u,&v,&x);
        add(u,v,x);
        add(v,u,x);
        }
        if(n==||n==) {puts("");continue;}
        spfa();
    }
}