并查集例题02.带权并查集(poj1182)

Description

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。
现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述：
第一种说法是"1 X Y"，表示X和Y是同类。
第二种说法是"2 X Y"，表示X吃Y。
此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
1） 当前的话与前面的某些真的话冲突，就是假话；
2） 当前的话中X或Y比N大，就是假话；
3） 当前的话表示X吃X，就是假话。
你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。

Input

第一行是两个整数N和K，以一个空格分隔。
以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。
若D=1，则表示X和Y是同类。
若D=2，则表示X吃Y。

Output

只有一个整数，表示假话的数目。

Sample Input

100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5

Sample Output

3

思路：

　　这道题为经典的带权并查集例题， 动物间的相对关系有三种可能：同类， 吃， 被吃

于是可以这样创建一个数组 relation[]，同时构造数组pre[]， pre[i]表示i的父节点。 　　relation[i]=0表示 i 与 pre[i] 同类， =1表示 i 吃 pre[i] ， =2表示 pre[i] 吃 i。

　　关于路径压缩：(find函数)， 我们可以发现权值（关系对应的值） 并不是直接累加， 但找规律后可以发现 A->C = (A->B + B->C) % 3，因此关系值的更新需要累加再模3。 find函数如下：

 int find(int x) {
     if (x != pre[x]) {
         int px = find(pre[x]);
         relation[x] = (relation[x] + relation[pre[x]]) % ;
         pre[x] = px;
     }
     return pre[x];
 }

　　至于合并过程， 从上面的规律可知， 只是在一般带权并查集的合并基础上取模

一般带权并查集的合并思路：

------>

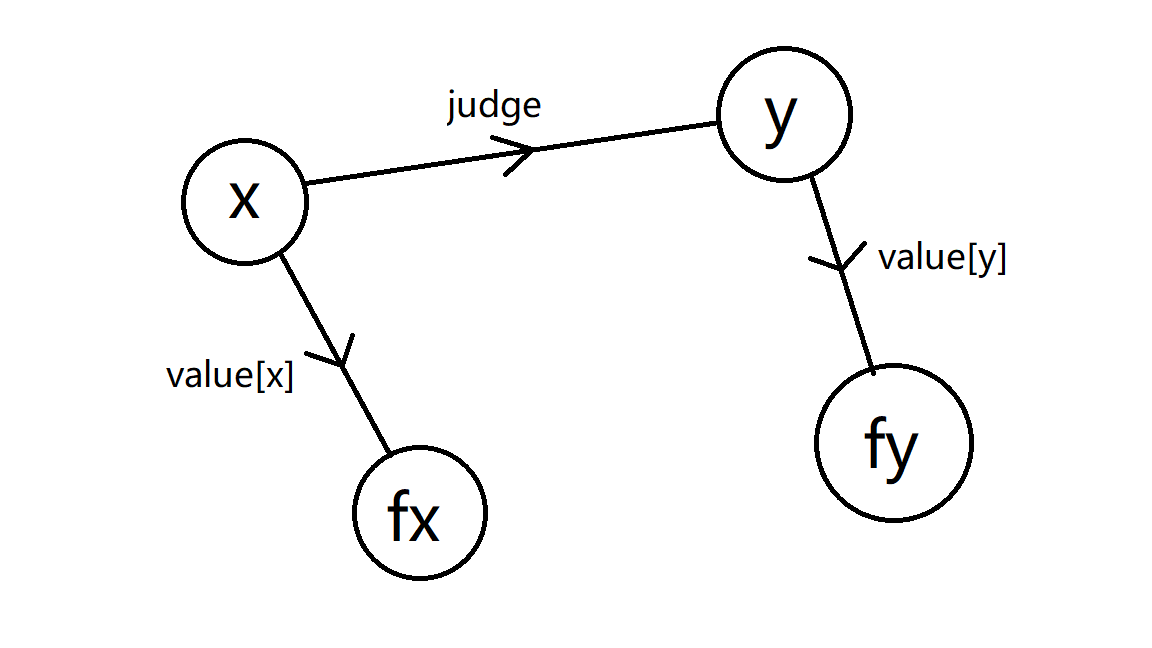 if (fx != fy) {
     pre[fx] = fy;
     value[fx] = judge + value[y] - value[x]
 }

总体上， c语言代码如下：

 #include <stdio.h>
 #include <string.h>
 #define maxn 50010
 int relation[maxn], pre[maxn];
 // relation[i] =    0: i与pre[i]为同类   1: i吃pre[i]   2: pre[i]吃i
 
 void init() {
     for (int i = ; i < maxn; i++) {
         relation[i] = ;
         pre[i] = i;
     }
 }
 
 int find(int x) {
     if (x != pre[x]) {
         int px = find(pre[x]);
         relation[x] = (relation[x] + relation[pre[x]]) % ;
         pre[x] = px;
     }
     return pre[x];
 }
 
 int jion(int x, int y, int judge) {
     int fx = find(x);
     int fy = find(y);
     if (fx == fy) {
         if ((relation[x] - relation[y] + ) %  != judge)   return ;
         else    return ;
     }
     else {
         pre[fx] = fy;
         relation[fx] = (relation[y] + judge - relation[x] + ) % ;
     }
     return ;
 }
 
 int main() {
     int N, K, x, y, judge, ans = ;
     scanf("%d%d", &N, &K);
     init();
     for (int i = ; i < K; i++) {
         scanf("%d%d%d", &judge, &x, &y);
         if (x > N || y > N || (x == y && judge == )) {
             ans++;
             continue;
         }
         if (jion(x, y, judge-)) {
             ans++;
         }
     }
     printf("%d\n", ans);
     return ;
 }