CF 149D Coloring Brackets（区间DP，好题，给配对的括号上色，求上色方案数，限制条件多，dp四维）

1、http://codeforces.com/problemset/problem/149/D

2、题目大意

给一个给定括号序列，给该括号上色，上色有三个要求

1、只有三种上色方案，不上色，上红色，上蓝色

2、每对括号必须只能给其中的一个上色

3、相邻的两个不能上同色，可以都不上色

求0-len-1这一区间内有多少种上色方案，很明显的区间DP

dp[l][r][i][j]表示l-r区间两端颜色分别是i,j的方案数

0代表不上色，1代表上红色，2代表上蓝色

对于l-r区间，有3种情况

1、if(l+1==r) 说明就只有一对，那么dp[l][r][0][1]=1;

        dp[l][r][1][0]=1;

        dp[l][r][0][2]=1;

        dp[l][r][2][0]=1;

2、if(l与r是配对的)

递归（l+1，r-1）

状态转移dp[l][r][0][1]=(dp[l][r][0][1]+dp[l+1][r-1][i][j])%mod; dp[l][r][1][0]=(dp[l][r][1][0]+dp[l+1][r-1][i][j])%mod;

dp[l][r][0][2]=(dp[l][r][0][2]+dp[l+1][r-1][i][j])%mod; dp[l][r][2][0]=(dp[l][r][2][0]+dp[l+1][r-1][i][j])%mod;

3、if(l与r不配对)

dp[l][r][i][j]=(dp[l][r][i][j]+(dp[l][p][i][k]*dp[p+1][r][q][j])%mod)%mod;

3、题目：

D. Coloring Brackets

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Once Petya read a problem about a bracket sequence. He gave it much thought but didn't find a solution. Today you will face it.

You are given string s. It represents a correct bracket sequence. A correct bracket sequence is the sequence of opening ("(") and closing (")")
brackets, such that it is possible to obtain a correct mathematical expression from it, inserting numbers and operators between the brackets. For example, such sequences as "(())()" and "()"
are correct bracket sequences and such sequences as ")()" and "(()" are not.

In a correct bracket sequence each bracket corresponds to the matching bracket (an opening bracket corresponds to the matching closing bracket and vice versa). For example, in a bracket sequence shown of the figure below, the third bracket corresponds to the
matching sixth one and the fifth bracket corresponds to the fourth one.

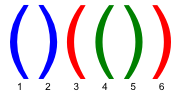
You are allowed to color some brackets in the bracket sequence so as all three conditions are fulfilled:

• Each bracket is either not colored any color, or is colored red, or is colored blue.
• For any pair of matching brackets exactly one of them is colored. In other words, for any bracket the following is true: either it or the matching bracket that corresponds to it is colored.
• No two neighboring colored brackets have the same color.

Find the number of different ways to color the bracket sequence. The ways should meet the above-given conditions. Two ways of coloring are considered different if they differ in the color of at least one bracket. As the result can be quite large, print it modulo 1000000007 (10⁹ + 7).

Input

The first line contains the single string s (2 ≤ |s| ≤ 700) which represents a correct bracket sequence.

Output

Print the only number — the number of ways to color the bracket sequence that meet the above given conditions modulo 1000000007 (10⁹ + 7).

Sample test(s)

Input

(())

Output

12

Input

(()())

Output

40

Input

()

Output

4

Note

Let's consider the first sample test. The bracket sequence from the sample can be colored, for example, as is shown on two figures below.

 

The two ways of coloring shown below are incorrect.

 

4、AC代码：

[cpp] view
plaincopy

1. #include<stdio.h>
2. #include<string.h>
3. #include<algorithm>
4. using namespace std;
5. #define N 705
6. #define mod 1000000007
7. char s[N];
8. int match[N];
9. int tmp[N];
10. long long dp[N][N][3][3];
     //注意用longlong
11. void getmatch(int len)
12. {
13. int p=0;
14. for(int i=0; i<len; i++)
15. {
16. if(s[i]=='(')
17. tmp[p++]=i;
18. else
19. {
20. match[i]=tmp[p-1];
21. match[tmp[p-1]]=i;
22. p--;
23. }
24. }
25. }
26. void dfs(int l,int r)
27. {
28. if(l+1==r)
29. {
30. dp[l][r][0][1]=1;
31. dp[l][r][1][0]=1;
32. dp[l][r][0][2]=1;
33. dp[l][r][2][0]=1;
34. return ;
35. }
36. if(match[l]==r)
37. {
38. dfs(l+1,r-1);
39. for(int i=0;i<3;i++)
40. {
41. for(int j=0;j<3;j++)
42. {
43. if(j!=1)
44. dp[l][r][0][1]=(dp[l][r][0][1]+dp[l+1][r-1][i][j])%mod;
45. if(i!=1)
46. dp[l][r][1][0]=(dp[l][r][1][0]+dp[l+1][r-1][i][j])%mod;
47. if(j!=2)
48. dp[l][r][0][2]=(dp[l][r][0][2]+dp[l+1][r-1][i][j])%mod;
49. if(i!=2)
50. dp[l][r][2][0]=(dp[l][r][2][0]+dp[l+1][r-1][i][j])%mod;
51. }
52. }
53. return ;
54. }
55. else
56. {
57. int p=match[l];
58. dfs(l,p);
59. dfs(p+1,r);
60. for(int i=0;i<3;i++)
61. {
62. for(int j=0;j<3;j++)
63. {
64. for(int k=0;k<3;k++)
65. {
66. for(int q=0;q<3;q++)
67. {
68. if(!((k==1 && q==1) || (k==2 && q==2)))
69. dp[l][r][i][j]=(dp[l][r][i][j]+(dp[l][p][i][k]*dp[p+1][r][q][j])%mod)%mod;
70. }
71. }
72. }
73. }
74. }
75. }
76. int main()
77. {
78. while(scanf("%s",s)!=EOF)
79. {
80. int len=strlen(s);
81. getmatch(len);
82. memset(dp,0,sizeof(dp));
83. dfs(0,len-1);
84. long long ans=0;
85. for(int i=0;i<3;i++)
86. {
87. for(int j=0;j<3;j++)
88. {
89. ans=(ans+dp[0][len-1][i][j])%mod;
90. }
91. }
92. printf("%ld\n",ans);
93. }
94. return 0;
95. }