obdg反汇编破解crackme

obdg是一个反汇编软件

直接将要反汇编的exe文件拖入或者file->open打开文件，等待一段时间就会显示出来

界面中分别为汇编代码（程序内存内容），寄存器内容，数据内存内容，栈内容

代码界面的左侧是内存地址，右侧是代码的描述

步骤一：修改程序使注册一直成功

在分析程序反汇编代码之前：

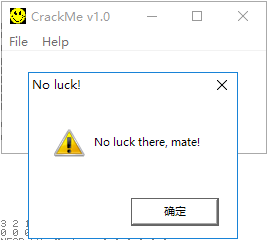
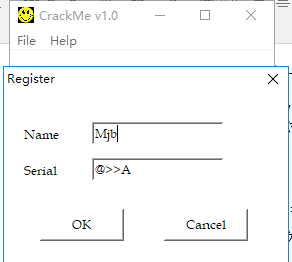
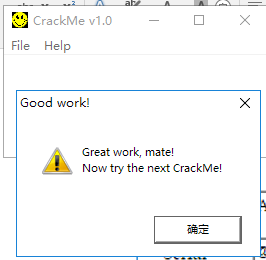
在该程序中，打开注册页面，随意输入信息并点击注册会弹出对话框：

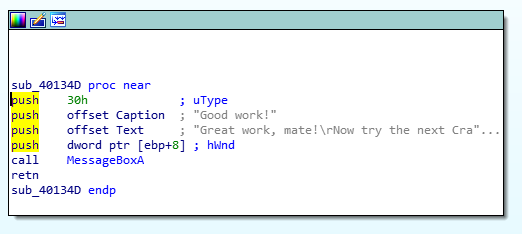
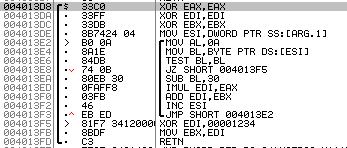
查看反汇编代码：

可以通过查看反编译之后的文字信息来确定部分代码的作用

这两段应该是分别对应成功注册和未成功注册的弹窗内容

可以看到，在push相应内容后调用了相同的程序段：MessageBoxA，应该是用于弹出指定栈内容的对话框。

猜测相关部分的逻辑：

那么这段功能的逻辑应该是有一个判断语句，根据结果是否为真分别跳转到上面图中的两段代码的push30处

确定要做的事：

只需要找到跳转到这两段程序的指令，并将判断条件修改为相反即可

遇到的问题：

直接在代码中找没有找到对应的跳转语句，执行step into会进入某些调用的API中跳不回来，执行step over又会执行到某些地方执行不下去。

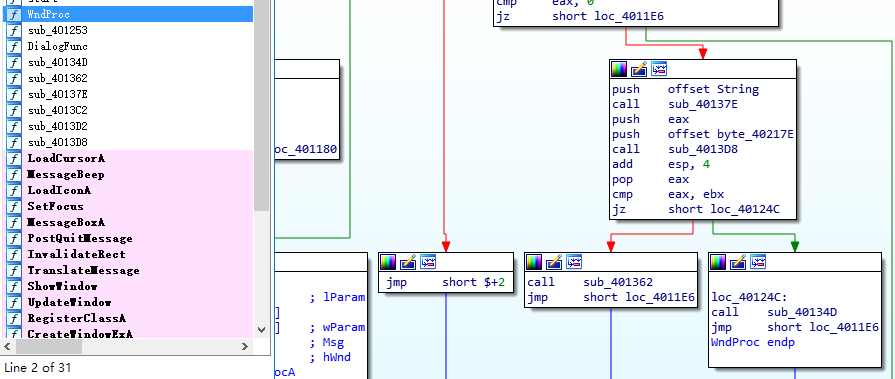
用软件IDA pro反汇编得到了程序的逻辑图，在逻辑图中找到了对应成功注册的子程序。

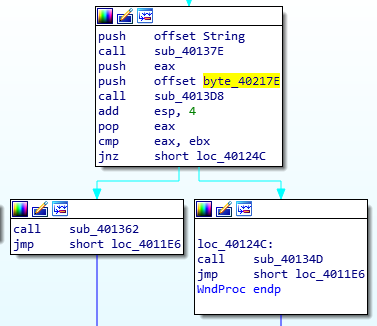
接下来找到那部分代码调用了它：

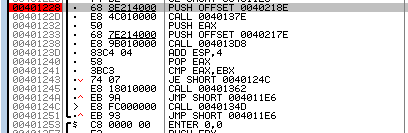
可以看到调用者有一个cmp和一个jz语句，而且另一分支调用的子程序正是注册失败弹窗的功能，那么这里的判断就应该是要找的语句

打开代码视图：

找到对应的语句的内存地址为00401243

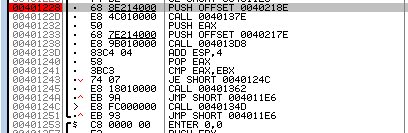
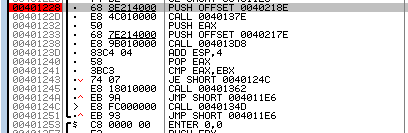
然后在odbg中找到对应的部分：

该语句跳转到0040124C，而0040124C又跳转到0040134D，即成功注册的弹窗

那么上面直接odbg中找的时候是没找到，而不是没有。直接找的时候误以为一定会有语句要求跳转到注册失败的语句（00401369），但是事实上程序的逻辑是判断条件正确就跳转到0040134D（成功注册），而失败的时候就直接顺序执行下去没有跳转语句。

修改程序二进制文件：

利用软件：Ultraedit

首先要找到对应的语句所在的具体存储位置：

文件偏移地址 = 虚拟内存地址(VA)- 装载基址(Image Base) - 节偏移

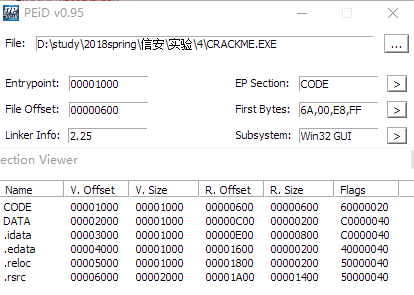
节偏移可以通过软件peid确定：V.Offset-R.Offset

所以文件偏移地址为：00401243-00400000-(00001000-00000600)=00000843

找到对应的位置，可以发现00000843和00000844正好是该跳转语句

修改为75 07：

生成的exe文件结果：

步骤二：寻找能成功注册软件的序列号

利用IDApro可以更方便的发现程序的结构：

下面的两个分别是输出成功注册和失败注册的弹窗，那么上面的子程序很可能就是处理在程序界面输入的name和serial，称之为子程序match

在OllyDbg中，在00401228处（即上面的子程序match起点处）设置断点单步执行，发现有以下的处理过程：

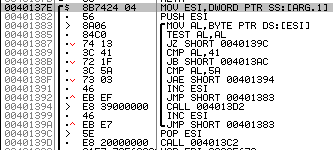
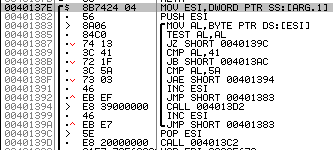
首先将name压栈，调用函数0040137E

该函数将按照name的每一位循环：

如果比’A’的ASSIC码值低就跳转到004013AC，这是注册失败时输出错误信息的子程序。

否则继续和’Z’比较，比‘Z’大，调用函数004013D2，作用为将ASSIC码减20，那么如果这个字符是小写字母，就会转化为相应的大写字母并存入

那么这部分的含义就是，循环判断所有name中的字符，如果符合是字母的条件就将字母转化为大写字母

全部判断完之后，调用004013C2，将所有字母的ASSIC码值加起来，返回。

继续将结果和00005678异或，结果放在EAX中

处理完name之后就将结果压栈，继而调用004013D8处理serial

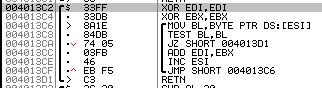
函数作用：

EDI初始化为0

For：将密码的每一位

将EDI乘10

减30加在EDI中，

结果和00001234（dec4660）XOR并存入EBX

处理完serial之后将name和serial的结果比较，如果相等就注册成功，否则注册失败

注册的内容不是唯一的，只要符合条件即可

假设name是”mjb”，那么序列号需要满足：

先将序列号处理：对序列号从前到后的每一位，减去30H加上sum乘AH作为新的sum，sum初始化为0

则sum满足：

‘A‘ xor 00005678H =sum xor 00001234H

寻找这样的sum，为17557D

分解为(((16*10+14)*10+14)*10+17)

每一位加上30H即48D为64/62/62/65，对应的字符为”@>>A”

那么这样的一个注册将会成功：

Mjb//无所谓大小写

@>>A