Spark MLlib回归算法LinearRegression

算法说明

　　线性回归是利用称为线性回归方程的函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析方法，只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归，在实际情况中大多数都是多元回归。

　　线性回归（Linear Regression）问题属于监督学习（Supervised Learning）范畴，又称分类（Classification）或归纳学习（Inductive Learning）。这类分析中训练数据集中给出的数据类型是确定的。机器学习的目标是，对于给定的一个训练数据集，通过不断的分析和学习产生一个联系属性集合和类标集合的分类函数（Classification Function）或预测函数）Prediction Function），这个函数称为分类模型（Classification Model——或预测模型（Prediction Model）。通过学习得到的模型可以是一个决策树、规格集、贝叶斯模型或一个超平面。通过这个模型可以对输入对象的特征向量预测或对对象的类标进行分类。

　　回归问题中通常使用最小二乘（Least Squares）法来迭代最优的特征中每个属性的比重，通过损失函数（Loss Function）或错误函数（Error Function)定义来设置收敛状态，即作为梯度下降算法的逼近参数因子。

实例介绍

　　该例子给出了如何导入训练集数据，将其解析为带标签点的RDD，然后使用了LinearRegressionWithSGD 算法来建立一个简单的线性模型来预测标签的值，最后计算了均方差来评估预测值与实际值的吻合度。

　　线性回归分析的整个过程可以简单描述为如下三个步骤：

　　（1）寻找合适的预测函数，即上文中的 h(x) ，用来预测输入数据的判断结果。这个过程是非常关键的，需要对数据有一定的了解或分析，知道或者猜测预测函数的“大概”形式，比如是线性函数还是非线性函数，若是非线性的则无法用线性回归来得出高质量的结果。

　　（2）构造一个Loss函数（损失函数），该函数表示预测的输出（h）与训练数据标签之间的偏差，可以是二者之间的差（h-y）或者是其他的形式（如平方差开方）。综合考虑所有训练数据的“损失”，将Loss求和或者求平均，记为 J(θ) 函数，表示所有训练数据预测值与实际类别的偏差。

　　（3）显然， J(θ) 函数的值越小表示预测函数越准确（即h函数越准确），所以这一步需要做的是找到 J(θ) 函数的最小值。找函数的最小值有不同的方法，Spark中采用的是梯度下降法（stochastic gradient descent，SGD)。

程序代码

import org.apache.log4j.{Level, Logger}

import org.apache.spark.{SparkContext, SparkConf}

import org.apache.spark.mllib.regression.LinearRegressionWithSGD

import org.apache.spark.mllib.regression.LabeledPoint

import org.apache.spark.mllib.linalg.Vectors

object LinearRegression {

  def main(args:Array[String]): Unit ={

    // 屏蔽不必要的日志显示终端上

    Logger.getLogger("org.apache.spark").setLevel(Level.ERROR)

    Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)

    // 设置运行环境

    val conf = new SparkConf().setAppName("Kmeans").setMaster("local[4]")

    val sc = new SparkContext(conf)

    // Load and parse the data

    val data = sc.textFile("/home/hadoop/upload/class8/lpsa.data")

    val parsedData = data.map { line =>

      val parts = line.split(',')

      LabeledPoint(parts().toDouble, Vectors.dense(parts().split(' ').map(_.toDouble)))

    }

    // Building the model

    val numIterations =

    val model = LinearRegressionWithSGD.train(parsedData, numIterations)

    // Evaluate model on training examples and compute training error

    val valuesAndPreds = parsedData.map { point =>

      val prediction = model.predict(point.features)

      (point.label, prediction)

    }

    val MSE = valuesAndPreds.map{ case(v, p) => math.pow((v - p), )}.reduce (_ + _) / valuesAndPreds.count

    println("training Mean Squared Error = " + MSE)

    sc.stop()

  }

}

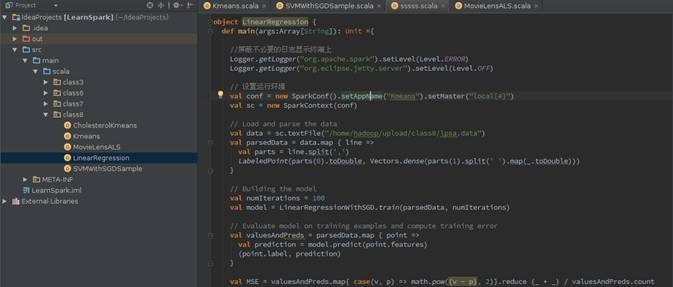
执行情况

　　第一步启动Spark集群

$cd /app/hadoop/spark-1.1.

$sbin/start-all.sh

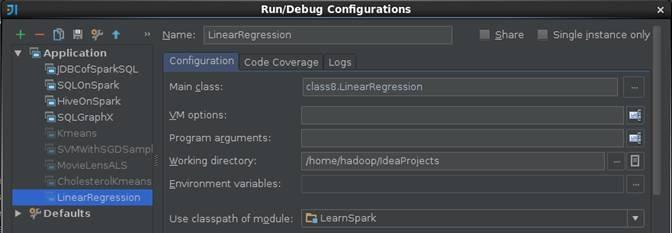
　　第二步在IDEA中设置运行环境

在IDEA运行配置中设置LinearRegression运行配置，由于读入的数据已经在程序中指定，故在该设置界面中不需要设置输入参数

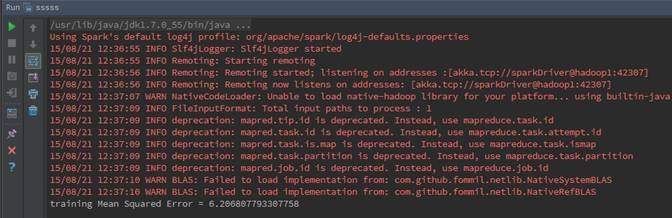
　　第三步执行并观察输出