C/C++ | 并查集:用于检查一个图上有没有环
没有环的过程分析: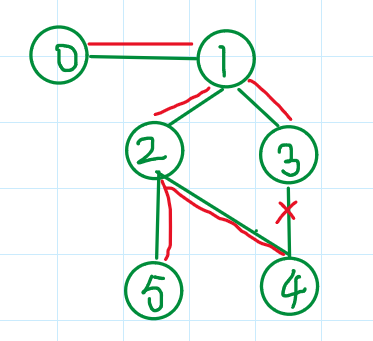
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#define VERTICES 6
#define LINE 5
using namespace std; /*
parent:数组解决并查集合并问题
VERTICES:设定的顶点数
LINE:设定的边数
*/
void initialise(int *parent)
{
//用于parent数组的初始化
int i;
for(i=0;i<VERTICES;i++)
{
parent[i]=-1;
}
}
int find_root(int x,int parent[])
{
//用来查找根节点
int x_root = x;
while(parent[x_root] != -1)
{
x_root = parent[x_root];
}
return x_root; }
int union_vertices(int x,int y,int parent[])
{
//用于合并两个集合 。返回0:合并成功,返回1:合并失败
int x_root=find_root(x,parent);
int y_root=find_root(y,parent);
printf("x:当前数是%d,他的parent是:%d\n",x,x_root);
printf("y:当前数是%d,他的parent是:%d\n",y,y_root); if(x_root==y_root)
{
return 0;
}
else
{
parent[x_root]=y_root;//将x连到y上
return 1;
} }
int main()
{
int parent[VERTICES]={0};
initialise(parent);
int edges[LINE][2] = {
{0,1},{1,2},{1,3},
{2,4},{2,5}
};
for(int i=0;i<LINE;++i)
{
int x=edges[i][0];
int y=edges[i][1];
if(union_vertices(x,y,parent)==0)
{
printf("存在环");
exit(0);
}
}
printf("没有环");
return 0;
}
最后一次执行了“parent[x_root]=y_root;”,所以4的parent变成了5
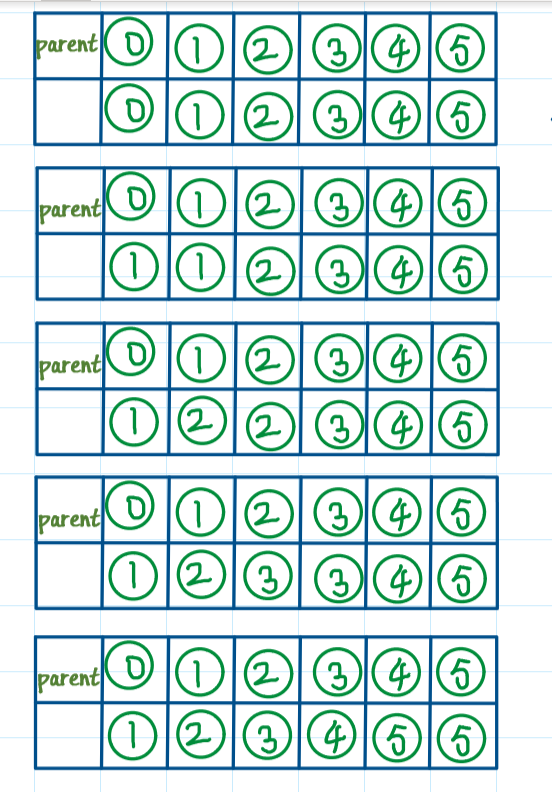
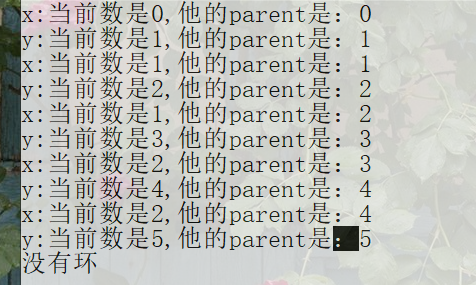
存在环的过程分析:
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#define VERTICES 6
#define LINE 6
using namespace std; /*
parent:数组解决并查集合并问题
VERTICES:设定的顶点数
LINE:设定的边数
*/
void initialise(int *parent)
{
//用于parent数组的初始化
int i;
for(i=0;i<VERTICES;i++)
{
parent[i]=-1;
}
}
int find_root(int x,int parent[])
{
//用来查找根节点
int x_root = x;
while(parent[x_root] != -1)
{
x_root = parent[x_root];
}
return x_root; }
int union_vertices(int x,int y,int parent[])
{
//用于合并两个集合 。返回0:合并成功,返回1:合并失败
int x_root=find_root(x,parent);
int y_root=find_root(y,parent);
printf("x:当前数是%d,他的parent是:%d\n",x,x_root);
printf("y:当前数是%d,他的parent是:%d\n",y,y_root); if(x_root==y_root)
{
return 0;
}
else
{
parent[x_root]=y_root;//将x连到y上
return 1;
} }
int main()
{
int parent[VERTICES]={0};
initialise(parent);
int edges[LINE][2] = {
{0,1},{1,2},{1,3},
{2,4},{2,5},{3,4}
};
for(int i=0;i<LINE;++i)
{
int x=edges[i][0];
int y=edges[i][1];
if(union_vertices(x,y,parent)==0)
{
printf("存在环");
exit(0);
}
}
printf("没有环");
return 0;
}
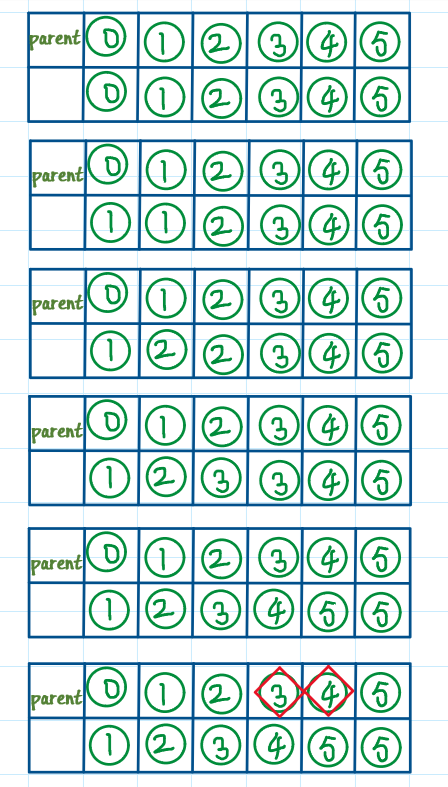
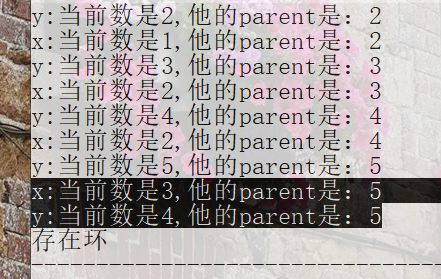
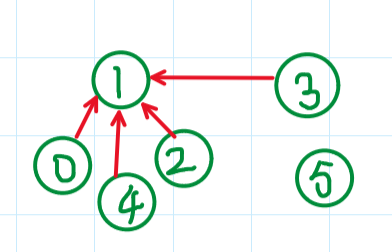
最后一次没有执行“parent[x_root]=y_root;”
路径压缩:
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#define VERTICES 6
#define LINE 6
using namespace std; void initialise(int *parent,int rank[])
{ int i;
for(i=0;i<VERTICES;i++)
{
parent[i]=-1;
rank[i]=0;
}
}
int find_root(int x,int parent[])
{ int x_root = x;
while(parent[x_root] != -1)
{
x_root = parent[x_root];
}
return x_root; }
int union_vertices(int x,int y,int parent[],int rank[])
{ int x_root=find_root(x,parent);
int y_root=find_root(y,parent);
printf("x:当前数是%d,他的parent是:%d,他的rank是:%d\n",x,x_root,rank[x]);
printf("y:当前数是%d,他的parent是:%d,他的rank是:%d\n",y,y_root,rank[y]); if(x_root==y_root)
{
return 0;
}
else
{
if(rank[x_root] > rank[y_root])
{
parent[y_root]=x_root;
}
else if(rank[y_root]>rank[x_root])
{
parent[x_root]=y_root;
}
else
{
parent[x_root]=y_root;
rank[y_root]++;
}
return 1;
} }
int main()
{
int parent[VERTICES]={0};
int rank[VERTICES]={0};
initialise(parent,rank);
int edges[LINE][2] = {
{0,1},{1,2},{1,3},
{2,4},{2,5},{3,4}
};
for(int i=0;i<LINE;++i)
{
int x=edges[i][0];
int y=edges[i][1];
if(union_vertices(x,y,parent,rank)==0)
{
printf("存在环");
exit(0);
}
}
printf("没有环");
return 0;
}
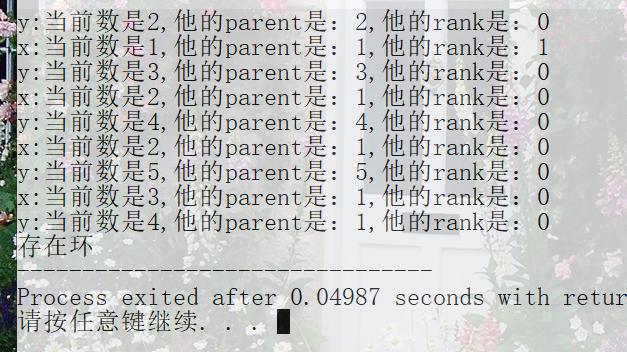
C/C++ | 并查集:用于检查一个图上有没有环的更多相关文章
- 【并查集的另一个思考方向】POJ1456
POJ1456 这个题一看好像就是用贪心做啊,一个结构体,拍一下序,vis数组一遍遍扫荡,最后输出值,没错,贪心的确能做出来,而这类题目也能应用并查集,实现得思想也是贪心 #include <i ...
- poj 1182 食物链 并查集的又一个用法
食物链 Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 41584 Accepted: 12090 Descripti ...
- 线段树 or 并查集 (多一个时间截点)
There is a company that has N employees(numbered from 1 to N),every employee in the company has a im ...
- D. Restructuring Company 并查集 + 维护一个区间技巧
http://codeforces.com/contest/566/problem/D D. Restructuring Company time limit per test 2 seconds m ...
- 【PAT甲级】1013 Battle Over Cities (25 分)(并查集,简单联通图)
题意: 输入三个整数N,M,K(N<=1000,第四个数据1e5<=M<=1e6).有1~N个城市,M条高速公路,K次询问,每次询问输入一个被敌军占领的城市,所有和该城市相连的高速公 ...
- LeetCode:并查集
并查集 这部分主要是学习了 labuladong 公众号中对于并查集的讲解,文章链接如下: Union-Find 并查集算法详解 Union-Find 算法怎么应用? 概述 并查集用于解决图论中「动态 ...
- 【POJ 1182 食物链】并查集
此题按照<挑战程序设计竞赛(第2版)>P89的解法,不容易想到,但想清楚了代码还是比较直观的. 并查集模板(包含了记录高度的rank数组和查询时状态压缩) *; int par[MAX_N ...
- codeforces 1023 D. Array Restoration 并查集
D. Array Restoration time limit per test 1 second memory limit per test 256 megabytes input standard ...
- POJ 1703 Find them, Catch them【种类/带权并查集+判断两元素是否在同一集合/不同集合/无法确定+类似食物链】
The police office in Tadu City decides to say ends to the chaos, as launch actions to root up the ...
随机推荐
- 2019了,给自己立一个flag吧
新年伊始,元旦已过,虽然有迟了,但是,相对于整年来说,还是比较早.年度总结,年度规划,除过上交的报告以外,还得自己给自己立个flag,一次来督促自己,而不是为了别的.做这些事,不仅仅是为了能更好的工作 ...
- Generative Model vs Discriminative Model
In this post, we are going to compare the two types of machine learning models-generative model and ...
- Web前端开发 --》 如何实现页面同时在移动端和pc端的兼容问题
很简单,只需要在html文件中对你引入的css进行一个类似于媒体查询的操作 <!DOCTYPE html> <html lang="en"> <hea ...
- js提交图片转换为base64
$("#picAjax").change(function () { var strs = ""; var file = $("#picAjax&qu ...
- “希希敬敬对”队软件工程第九次作业-beta冲刺第一次随笔
队名: “希希敬敬对” 龙江腾(队长) 201810775001 杨希 201810812008 何敬上 201810812004 今日讨论会议照片一张: 每个人 ...
- mysql字符串拆分实现split功能
转自:https://blog.csdn.net/pjymyself/article/details/81668157有分隔符的字符串拆分题目要求数据库中 num字段值为: 实现的效果:需要将一行数据 ...
- MongoDB查询系统
首先,我们先向集合(collections)中添加测试文档(documents).如下: > for(i=1;i<=5;i++) db.test.insert({x:i,y:i*i,z:6 ...
- npm基本介绍及使用
1.什么是npm npm全称node package manager,是node包管理和分发工具.可以理解为前端的maven.通过npm可以很方便的下载js库,管理前端工程.node已经集成npm工具 ...
- 小白学Python(18)——pyecharts 关系图 Graph
Graph-基本示例 import json import os from pyecharts import options as opts from pyecharts.charts import ...
- ASE Alpha Sprint - backend scrum 3
本次scrum于2019.11.7再sky garden进行,持续10分钟. 参与人: Zhikai Chen, Jia Ning, Hao Wang 请假: Xin Kang, Lihao Ran, ...
