hdu 5212 : Code【莫比乌斯】

题目链接

题给代码可以转化为下面的公式

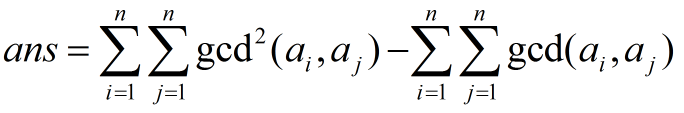
然后用F[n]记录公约数为n的(a[i],a[j])对数，用f[n]记录最大公约数为n的(a[i],a[j])对数

之后枚举最大公约数d

至于求F[n]，可以先将1~10000全部因数分解，用num[i]记录约数中包含i的a[x]的个数。对每一个a[i]，其每一个约数都对对应的num[i]贡献了1 。显然，F[n]=num[n]*num[n]

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

;
const int maxn=1e6;

];
];
];

void init()
{
    mu[]=;
    ;
    ;i<=maxn;i++)
    {
        if(!check[i])
        {
            prime[tot++]=i;
            mu[i]=-;
        }
        ;j<tot;j++)
        {
            if(i*prime[j]>maxn) break;
            check[i*prime[j]]=true;
            )
            {
                mu[i*prime[j]]=;
                break;
            }
            else
            {
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
}

int n;
];
LL num[];
vector<];
LL f[];
LL F[];

void init1()
{
    ;i<=;i++)
    {
        int j;
        ;j*j<i;j++)
            )
            {
                fac[i].push_back(j);
                fac[i].push_back(i/j);
            }
        if(j*j==i) fac[i].push_back(j);
        sort(fac[i].begin(),fac[i].end());
    }
}
void add(int x)
{
    ;i<fac[x].size();i++)
        num[fac[x][i]]++;
}

int gcd(int a,int b)
{
    return b? gcd(b,a%b): a;
}

//int calc()
//{
//    int res=0;
//    for(int i=1; i<=n; i++)
//        for(int j=1; j<=n; j++)
//        {
//            res+=gcd(a[i],a[j])*(gcd(a[i],a[j])-1);
//            res%=10007;
//        }
//    return res;
//}

int main()
{
    init();
    init1();
    while(~scanf("%d",&n))
    {
        memset(num,,sizeof(num));
        memset(f,,sizeof(f));
        ;i<=n;i++)
        {
            scanf("%d",&a[i]);
            add(a[i]);
        }
        LL ans1=,ans2=;
        ;i<=;i++)
            F[i]=num[i]*num[i];
        ;i<=;i++)
            ;i*j<=;j++)
                f[i]=(f[i]+mu[j]*F[i*j])%mod;
        ;i<=;i++)
        {
            ans1=(ans1+f[i]*i*i)%mod;
            ans2=(ans2+f[i]*i)%mod;
        }
        printf("%lld\n",((ans1-ans2)%mod+mod)%mod);
//        cout<<calc()<<endl;
    }
}