【题解】Editor [HDU4699]

【题解】Editor [HDU4699]

---

传送： \(Editor\) \([HDU4699]\)

【题目描述】

有一个维护整数序列的强大编辑器，初始状态为空，下面提供五种不同的操作，给出的总操作次数 \(m \leqslant 1e6\) 。

\(“I,x”:\) 在光标后面添加一个整数 \(x\)；

\(“D”:\) 删除光标前面的整数； \([Backspace]\)

\(“L”:\) 光标向左移动一个单位，除非它已在第一个位置； \([←]\)

\(“R”:\) 光标向右移动一个单位，除非它已在最后一个位置； \([→]\)

\(“Q,k”:\) 输出位置在k之前的最大前缀和。

【样例】

输入：
8
I 2
I -1
I 1
Q 3
L
D
R
Q 2

输出：
2
3

【数据范围】

\(1 \leqslant Q \leqslant 1e6\) \(,\) \(\left| x \right| \leqslant 1000\)

---

【分析】

对顶栈的炒鸡大水题

但毕竟当初花了那么对时间去搞栈，所以还是水写几篇题解吧...

仔细观察一下题目，问题的关键就在于\(“I”\)，\(“D”\)，即添加和删除，这里我们先换个词，插入（~~啊_恩~）和弹出。如果暂时不考虑光标左右移动的情况，那么每次删除的一定是最后一次插入的整数。后进先出，一进一出的动作都在序列尾进行，这不就是个栈么？

那么如何解决光标左右移动的情况呢？

我们可以设置两个栈 \(L\) 和 \(R\)，分别表示光标左右两边的所有数字，靠近光标左右两边的数为栈顶，序列首和序列尾为栈底。

对于每一次的操作：

插入\((“I,x”)：\)把 \(x\) 丢进 \(L\)。

删除\((“D”)：\)弹出 \(L\) 栈顶元素。

左移\((“L”)：\)弹出 \(L\) 栈顶元素，并丢进 \(R\)。

右移\((“R”)：\)弹出 \(R\) 栈顶元素，并丢进 \(L\)。

模拟一下。。。

当前的状态：

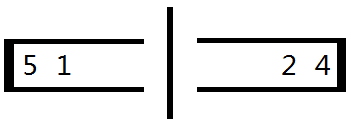
删除操作后的状态：

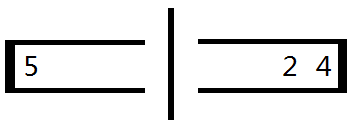
右移操作后的状态：

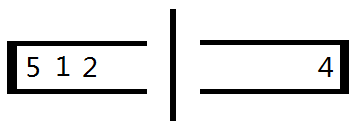
左移操作后的状态：

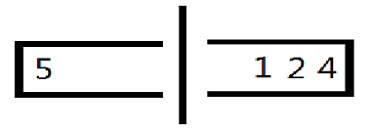
\((“Q,k”)\) 如何查询最大前缀和？

其实很简单，用一个变量 \(sum\) 表示当前位置的前缀和，再开一个数组 \(f[\) \(]\) 保存每个位置前面的最大前缀和。

当 \(L\) 中有元素 \(x\) 插入时，更新 \(sum\) 和 \(f[\) \(]\)，当有元素弹出时，只更新 \(sum\) 。

这道题有两种实现方法：\(STL\) 和手写栈。

不过呢，用 \(STL\) 速度慢，代码长......懂我什么意思了吧....

【Code】

【STL】

#include<iostream>
#include<cstdio>
#include<stack>
using namespace std;
const int N=1e6+5;
stack<int> L,R;
int m,x,t,f[N],sum;char a;
inline int Max(int x,int y){return x>y?x:y;}
int main(){
    while(scanf("%d",&m)>0){
        t=sum=0;//用t表示当前L中的元素个数，同时也是光标左边的位置
        while(!L.empty())L.pop();//清空两个栈
        while(!R.empty())R.pop();//QAQ,QWQ,QAQ
        f[0]=-0x7fffffff;//这个很重要，否则会WA一片
        while(m--){
            cin>>a;
            if(a=='I'){//添加
                scanf("%d",&x);
                L.push(x);++t;//左边新增一个数x
                f[t]=Max(f[t-1],sum+=x);//更新sum,f[tL]
            }
            else if(a=='D'&&!L.empty())sum-=L.top(),L.pop(),t--;//删除,sum也实时更新
            else if(a=='L'&&!L.empty()){//左移
                R.push(L.top());//左边减少一个数,放入右边
                sum-=L.top();//更新sum
                L.pop();t--;
            }
            else if(a=='R'&&!R.empty()){//右移
                L.push(R.top());t++;//右边减少一个数,放入左边
                f[t]=Max(f[t-1],sum+=R.top());//更新sum,f[tL]
                R.pop();
            }
            else if(a=='Q')scanf("%d",&x),printf("%d\n",f[x]);//查询
        }
    }
}

【手写栈】

#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e6+5;
int m,x,tL,tR,L[N],R[N],f[N],sum;char a;
inline int Max(int x,int y){return x>y?x:y;}
int main(){
    while(scanf("%d",&m)>0){
        tL=tR=sum=0;f[0]=-0x7fffffff;
        while(m--){
            cin>>a;
            if(a=='I'){
                scanf("%d",&x);
                L[++tL]=x;
                f[tL]=Max(f[tL-1],sum+=x);
            }
            if(a=='R'&&tR){
                x=L[++tL]=R[tR--];
                f[tL]=Max(f[tL-1],sum+=x);
            }
            if(a=='Q')scanf("%d",&x),printf("%d\n",f[x]);
            if(a=='L'&&tL){sum-=L[tL],R[++tR]=L[tL--];}
            if(a=='D'&&tL)sum-=L[tL--];
        }
    }
}