Codeforces Gym101246G：Revolutionary Roads（DFS+思维）

http://codeforces.com/gym/101246/problem/G

题意：有一个n个点m条边的有向图，现在可以修改某一条有向边使得其为无向边，问修改哪些边可以使得修改后的强连通分量的点数最多，输出。

思路：

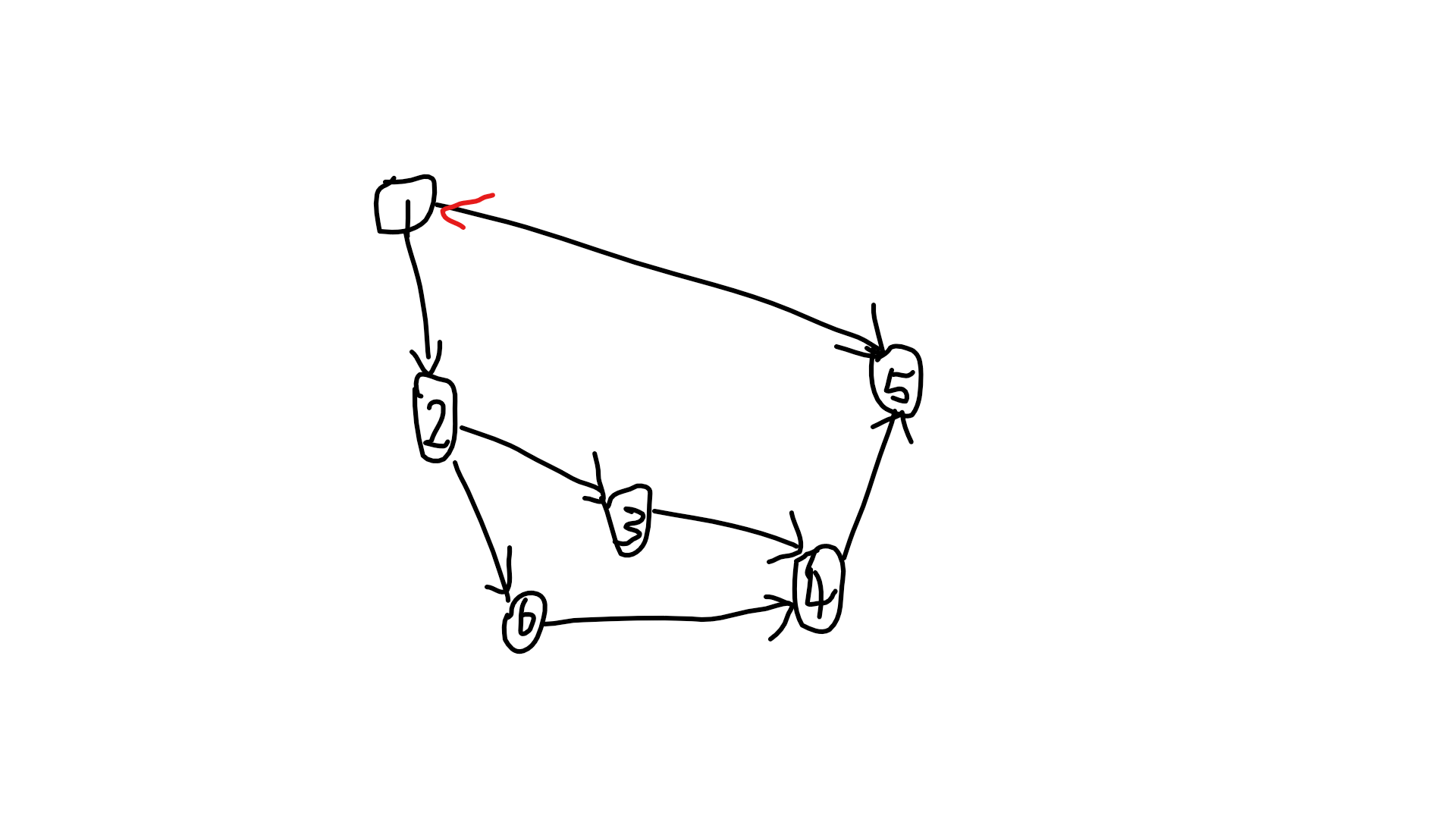
要使得修改边后的强连通分量的点数最多，假设当前修改的边的入点为u，出点为v，那么能在修改当前的边之后在强连通分量里面的点i，当且仅当修改边之前u能到达i并且i能到达v，然后修改之后，i就能通过v回到u，这样就是强连通的了。比如上面这个样例的1->5这条边，1（u）能到达1、2、3、4、6、5并且1、2、3、4、6、5能到达5（v），因此修改1->5这条边之后，整个图都是强连通的了。

判断点与点之间是否可达，就可以对每一个点都进行一下DFS，DFS中遍历到的点都是可达的。

处理出关系之后，就可以枚举边，判断对于当前的边，有哪些点可以在修改后的强连通分量里面。

时间复杂度为O（mn）。

注意：m可以为0！！！没有边的情况下，输出的点数应该是1而不是0！

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 #define M 20010
 #define N 1010
 struct Edge {
     int v, nxt;
 } edge[M];
 int vis[N], head[N], tot, mp[N][N], ans[M], u[M], v[M];

 void Add(int u, int v) { edge[tot] = (Edge) {v, head[u]}; head[u] = tot++; }

 void dfs(int u, int st) {
     for(int i = head[u]; ~i; i = edge[i].nxt) {
         int v = edge[i].v;
         if(vis[v]) continue;
         mp[st][v] = ;
         vis[v] = ; dfs(v, st);
     }
 }

 int main() {
     freopen("input.txt", "r", stdin);
     freopen("output.txt", "w", stdout);
     int n, m;
     scanf("%d%d", &n, &m);
     if(!m) { puts("1\n0"); return ; }
     memset(head, -, sizeof(head));
     for(int i = ; i <= m; i++) {
         scanf("%d%d", &u[i], &v[i]);
         Add(u[i], v[i]);
     }
     for(int i = ; i <= n; i++) {
         mp[i][i] = ; // 判断是否可达
         memset(vis, , sizeof(vis));
         vis[i] = ; dfs(i, i);
     }
     int res = , cnt = ;
     for(int i = ; i <= m; i++) {
         int now = ;
         for(int j = ; j <= n; j++) if(mp[u[i]][j] && mp[j][v[i]]) now++;
         if(now > res) { res = now; cnt = ; ans[++cnt] = i; }
         else if(now == res) ans[++cnt] = i;
     }
     printf("%d\n%d\n", res, cnt);
     for(int i = ; i <= cnt; i++) printf("%d ", ans[i]);
     return ;
 }