[考试反思]1023csp-s模拟测试84：精妙

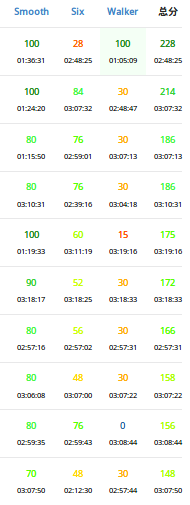
一套很奇怪的题。单调性+神仙dp/搜索+随机化。

但是说实在的，思路都很不错。

考场上显然乱搞没什么好说的。

虽说T2剪枝打错变量名掉了20分。。。

T1：Smooth

暴力各有不同，最暴力的想法就是往队列里不断扔。

有的元素会被扔多次导致队列元素过多。

像线性筛一样，从大到小枚举质因子，保证每个数只会被最大的质因子筛掉。

 #include<cstdio>
 #include<queue>
 using namespace std;
 priority_queue<long long,vector<long long>,greater<long long> >q;
 const int P[]={,,,,,,,,,,,,,,,};
 int main(){//freopen("ex_smooth1.in","r",stdin);
     int k,b;
     scanf("%d%d",&b,&k);
     q.push();
     k--;
     while(k--){
         long long x=q.top();q.pop();
         for(int i=b;i;--i)if(x%P[i]==){q.push(x*P[i]);break;}
             else q.push(x*P[i]);
     }
     printf("%lld\n",q.top());
 }

T80

像蚯蚓一样，加入队列有单调性，所以不用优先队列。

开b个队列，每个队列i里存最大质因子是p_i的数。

 #include<cstdio>
 #include<queue>
 using namespace std;
 queue<long long>q[];
 const int P[]={,,,,,,,,,,,,,,,};
 int b,k;
 long long pop_push(){
     long long ans=q[].front(),bp=;
     for(int i=;i<=b;++i)if(q[i].front()<ans)ans=q[i].front(),bp=i;
     q[bp].pop();
     for(int i=b;i>=bp;--i)q[i].push(ans*P[i]);
     return ans;
 }
 int main(){
     scanf("%d%d",&b,&k);
     for(int i=;i<=b;++i)q[i].push(P[i]);
     k-=;
     while(k--)pop_push();
     printf("%lld\n",pop_push());
 }

T2：Six

先说暴力？

搜啊，好像没什么好说的。

发现每次加入的数的影响只与它含有哪几种质因子有关。

然后就可以愉快的搜了。

 #include<cstdio>
 #define mod 1000000007
 #define int long long
 int t[],knd,al[];long long n,rate[];
 int sch(int p){//if(p<=3)printf("%d\n",p);
     int ans=;
     for(int i=;i<<<knd;++i){
         int cov=;
         for(int j=;j<p;++j)if(i&al[j])cov++;
         if(cov>)continue;
         al[p]=i;
         ans=(ans+rate[i]*sch(p+))%mod;
     }
     return ans;
 }
 main(){
     scanf("%lld",&n);
     for(long long i=;i*i<=n;++i)if(n%i==){
         knd++;
         while(n%i==)n/=i,t[knd]++;
     }if(n!=)t[++knd]=;
     for(int i=;i<<<knd;++i){
         rate[i]=;
         for(int j=;j<=knd;++j)if(i&<<j-)(rate[i]*=t[j])%=mod;
     }
     printf("%lld\n",sch()-);
 }

T74

%%%ParisB的Six的状态定义。

首先我们可以发现，每个质因子的第一次被加入，至多会分6批。

我们考虑加入一个数的限制。

如果某一种因子已经被两个数包含，你还含有这个因子，就不合法。

如果你含有两个因子A和B，A和B被加入不在同一个数里（就是我上面说的“6批”），那么不合法。

如果在同一批里，那么你就只与那一批的一个数冲突，还是合法的。

所以你就记录一下每一个因子是在第几批加入的。8进制压位。

0：未被加入。

1～6：被在第1～6批加入。

7：已经被加入2次。

然后对于每一种状态，枚举$2^6$种可能的转移，不合法的情况只有上面2种。

总复杂度$2^{18} \times 2^6 \times 6$然而因为合法状态只有2100种，所以最终的复杂度大约是1e6的。

代码极短但是不易压行（否则逻辑极其混乱）

适度的常用位运算宏定义能使代码更加简单而清晰

 #include<cstdio>
 #define mod 1000000007
 #define s1 (k&1<<p-1)
 #define s2 (j>>3*p-3&7)
 int dp[],t[],cnt,ans;long long n,rate[];
 int main(){
     scanf("%lld",&n);
     for(long long i=;i*i<=n;++i)if(n%i==){
         cnt++;
         while(n%i==)n/=i,t[cnt]++;
     }if(n!=)t[++cnt]=;
     for(int i=;i<<<cnt;++i){
         rate[i]=;
         for(int j=;j<=cnt;++j)if(i&<<j-)rate[i]*=t[j];
     }
     dp[]=;
     for(int j=;j<<<cnt*;++j)if(dp[j]){
         ans=(ans+dp[j])%mod;
         for(int k=;k<<<cnt;++k){
             int x=,ns=j,m=;
             for(int p=;p<=cnt;++p)if(!s2&&s1){x=p;break;}
             for(int p=;p<=cnt;++p)if(s2&&s1)
                 if(s2==)goto F;
                 else if(!m)m=s2;
                 else if(m!=s2)goto F;
             for(int p=;p<=cnt;++p)if(s1)
                 if(s2)ns|=<<*p-;
                 else ns|=x<<*p-;
             dp[ns]=(dp[ns]+dp[j]*rate[k])%mod; F:;
         }
     }printf("%d\n",ans-);
 }

825B。快去%ParisB

T3：Walker

变化完之后的最终坐标是$(scale \ cos \theta \ x - scale\  sin \theta \ y +d_x,scale \ sin \theta\ x + scale \ cos\theta \ y +d_y)$

我们把$scale \ sin \theta$和$scale \ cos \theta$看做两个单独的变量，叫$a,b$吧

然后我们随便带两组数据进去就能解出$a,b,d_x,d_y$这四个变量

根据$sin^2\theta +cos^2\theta=1$，得到$a^2+b^2=scale^2$

所以我们就解出了$scale$,同时也就解出了$sin\theta$和$cos\theta$

然后问题在于怎么解出$\theta$。方法很多，我说一个。

根据$\frac{sin\theta}{cos\theta}=tan\theta$我们能知道$tan$值，利用$atan$函数得到一个$\theta$值。

然后我们再用$sin$函数算一下这个$\theta$的正弦值和上面那个$\frac{a}{scale}$是否一致。

如果一致，那么就对了，否则加一个$\pi$，转半圈就是了。（因为只根据$tan$得到的角度值可能刚好是相反的）

我们对于两个坐标求出的一组解拿去check，如果超过半数都是对的那么就完事，否则继续循环

因为有一半是正确的，所以你选出两个正确坐标的概率是$\frac{1}{4}$，不是很小，所以循环不会很多次。

 #include<bits/stdc++.h>
 using namespace std;
 #define ldb double
 int n;ldb x[],y[],_x[],_y[],mxt[][];
 void Gauss(){
     for(int i=;i<=;++i){
         ldb mx=mxt[i][i];int mxp=i;
         for(int j=i+;j<=;++j)if(fabs(mxt[j][i])>mx)mx=fabs(mxt[j][i]),mxp=j;
         if(mxp!=i)for(int j=i;j<=;++j)swap(mxt[i][j],mxt[mxp][j]);
         for(int j=;j>i;--j)for(int k=;k>=i;--k)mxt[j][k]-=mxt[j][i]/mxt[i][i]*mxt[i][k];
     }
     for(int i=;i;--i)for(int j=i-;j;--j)mxt[j][]-=mxt[i][]*mxt[j][i]/mxt[i][i];
     for(int i=;i;--i)mxt[i][]/=mxt[i][i];
 }
 int main(){
     scanf("%d",&n);srand(time());
     for(int i=;i<=n;++i)scanf("%lf%lf%lf%lf",&_x[i],&_y[i],&x[i],&y[i]);
     while(){
         int p1=rand()%n+,p2=rand()%n+,AC=;
         while(p1==p2)p2=rand()%n+;
         mxt[][]=x[p1];mxt[][]=;mxt[][]=;mxt[][]=-_y[p1];mxt[][]=+_x[p1];
         mxt[][]=y[p1];mxt[][]=;mxt[][]=;mxt[][]=+_x[p1];mxt[][]=+_y[p1];
         mxt[][]=x[p2];mxt[][]=;mxt[][]=;mxt[][]=-_y[p2];mxt[][]=+_x[p2];
         mxt[][]=y[p2];mxt[][]=;mxt[][]=;mxt[][]=+_x[p2];mxt[][]=+_y[p2];
         Gauss();
         ldb scale=mxt[][]*mxt[][]+mxt[][]*mxt[][];scale=sqrt(scale);
         ldb cosine=mxt[][]/scale,sine=mxt[][]/scale,theta=atan(sine/cosine),X=mxt[][],Y=mxt[][];
         if(scale>||scale<)continue;
         if(fabs(sin(theta)-sine)>1e-)theta+=.141592653589793238462643383279l;
         if(theta<-1e-)theta+=.141592653589793238462643383279L*;
         for(int i=;i<=n;++i)if(fabs(scale*cos(theta)*_x[i]-scale*sin(theta)*_y[i]+X-x[i])<1e-&&fabs(scale*sin(theta)*_x[i]+scale*cos(theta)*_y[i]+Y-y[i])<1e-)AC++;
         if(AC>=n+>>)return printf("%.18lf\n%.18lf\n%.18lf %.18lf\n",theta,scale,X,Y),;
     }
 }