Focal Loss 理解

本质上讲，Focal Loss 就是一个解决分类问题中类别不平衡、分类难度差异的一个 loss，总之这个工作一片好评就是了。

看到这个 loss，开始感觉很神奇，感觉大有用途。因为在 NLP 中，也存在大量的类别不平衡的任务。最经典的就是序列标注任务中类别是严重不平衡的，比如在命名实体识别中，显然一句话里边实体是比非实体要少得多，这就是一个类别严重不平衡的情况。

硬截断

整篇文章都是从二分类问题出发，同样的思想可以用于多分类问题。二分类问题的标准 loss 是交叉熵。

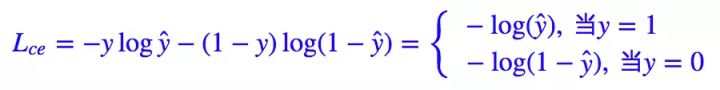
其中 y∈{0,1} 是真实标签，ŷ 是预测值。当然，对于二分类我们几乎都是用 sigmoid 函数激活 ŷ =σ(x)，所以相当于：

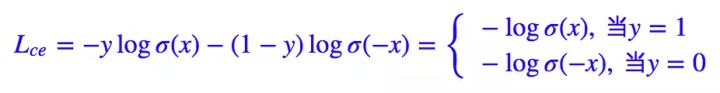
我们有 1−σ(x)=σ(−x)。

曾经针对“集中精力关注难分样本”这个想法提出了一个“硬截断”的 loss，形式为：

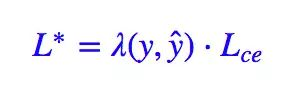
其中：

这样的做法就是：正样本的预测值大于 0.5 的，或者负样本的预测值小于 0.5 的，我都不更新了，把注意力集中在预测不准的那些样本，当然这个阈值可以调整。这样做能部分地达到目的，但是所需要的迭代次数会大大增加。

原因是这样的：以正样本为例，我只告诉模型正样本的预测值大于 0.5 就不更新了，却没有告诉它要“保持”大于 0.5，所以下一阶段，它的预测值就很有可能变回小于 0.5 了。当然，如果是这样的话，下一回合它又被更新了，这样反复迭代，理论上也能达到目的，但是迭代次数会大大增加。

所以，要想改进的话，重点就是“不只是要告诉模型正样本的预测值大于0.5就不更新了，而是要告诉模型当其大于0.5后就只需要保持就好了”。好比老师看到一个学生及格了就不管了，这显然是不行的。如果学生已经及格，那么应该要想办法要他保持目前这个状态甚至变得更好，而不是不管。

软化 loss

硬截断会出现不足，关键地方在于因子 λ(y,ŷ) 是不可导的，或者说我们认为它导数为 0，因此这一项不会对梯度有任何帮助，从而我们不能从它这里得到合理的反馈（也就是模型不知道“保持”意味着什么）。

解决这个问题的一个方法就是“软化”这个 loss，“软化”就是把一些本来不可导的函数用一些可导函数来近似，数学角度应该叫“光滑化”。这样处理之后本来不可导的东西就可导了，类似的算例还有梯度下降和EM算法：系出同源，一脉相承中的 kmeans 部分。我们首先改写一下 L∗。

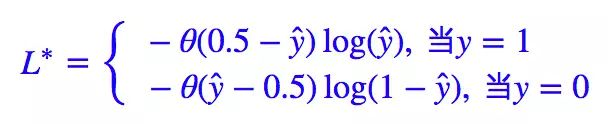
这里的 θ 就是单位阶跃函数：

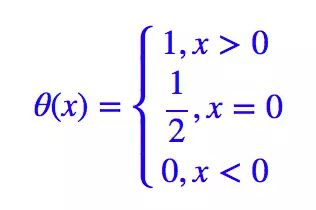
这样的 L∗ 跟原来的是完全等价的，由于 σ(0)=0.5，因此它也等价于：

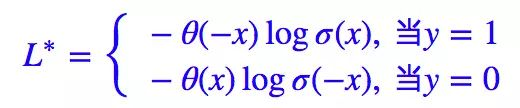
这时候思路就很明显了，要想“软化”这个 loss，就得“软化” θ(x)，而软化它就再容易不过，它就是 sigmoid 函数（不懂可以去看sigmoid图像）。我们有：

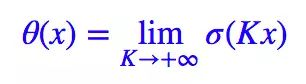
所以很显然，我们将 θ(x) 替换为 σ(Kx) 即可：

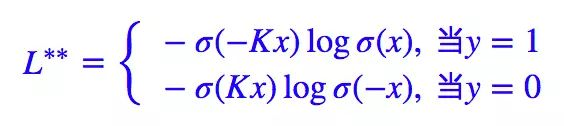
现在跟 Focal Loss 做个比较。

Focal Loss

Kaiming 大神的 Focal Loss 形式是：

如果落实到 ŷ =σ(x) 这个预测，那么就有：

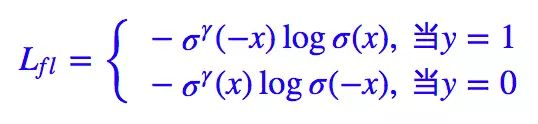
特别地，如果 K 和 γ 都取 1，那么 L∗∗=Lfl。

事实上 K 和 γ 的作用都是一样的，都是调节权重曲线的陡度，只是调节的方式不一样。注意L∗∗或 Lfl 实际上都已经包含了对不均衡样本的解决方法，或者说，类别不均衡本质上就是分类难度差异的体现。

比如负样本远比正样本多的话，模型肯定会倾向于数目多的负类（可以想象全部样本都判为负类），这时候，负类的 ŷ γ 或 σ(Kx) 都很小，而正类的 (1−ŷ )γ 或 σ(−Kx) 就很大，这时候模型就会开始集中精力关注正样本。

还有种理解方法，如果有8个类别，1个正类别，7个负类别，7个负类别加起来的loss大于了1个正类别的loss，而这个函数就是相当于调节的作用，将负样本的loss放低，正样本的loss放大。

当然，Kaiming 大神还发现对 Lfl 做个权重调整，结果会有微小提升。

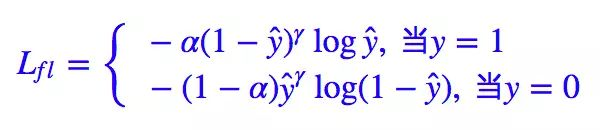
通过一系列调参，得到 α=0.25, γ=2（在他的模型上）的效果最好。注意在他的任务中，正样本是属于少数样本，也就是说，本来正样本难以“匹敌”负样本，但经过 (1−ŷ )γ 和 ŷγ 的“操控”后，也许形势还逆转了，还要对正样本降权。

不过我认为这样调整只是经验结果，理论上很难有一个指导方案来决定 α 的值，如果没有大算力调参，倒不如直接让 α=0.5（均等）。

多分类

Focal Loss 在多分类中的形式也很容易得到，其实就是：

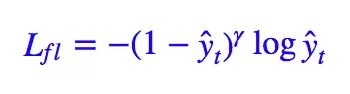
ŷt 是目标的预测值，一般就是经过 softmax 后的结果。那我自己构思的 L∗∗ 怎么推广到多分类？也很简单：

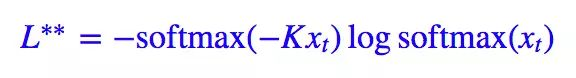
这里 xt 也是目标的预测值，但它是 softmax 前的结果。

参考：https://zhuanlan.zhihu.com/p/32423092