Delphi - Windows系统下，Delphi调用API函数和7z.dll动态库，自动把文件压缩成.tar.gz格式的文件

项目背景

应欧美客户需求，需要将文件压缩成.tar.gz格式的文件，并上传给客户端SFTP服务器。

你懂的，7-Zip软件的显著特点是文件越大压缩比越高，在Linux系统上相当于我们Windows系统上WinRAR或者好压软件一样的存在。

7-Zip软件下载与安装

网上下载相关安装包并完成安装，找到安装目录，复制7z.dll文件到D盘。

.bat文件的制作

通过7-Zip软件使用手册了解到，通过动态命令行调用7z.dll可以把文件压缩成.tar.gz格式的，实际上是先将文件压缩成.tar格式的文件，然后再把.tar格式的文件压缩成.gz格式的文件。

看如下代码：

a：在D盘新建两个文件夹，即WaitForCompress和Compressed

b：在D盘新建一个记事本文件，将如下代码复制进去，保存，退出，修改文件名为Run.bat

c：将7z.dll文件Copy到D盘与Run.bat在同一目录。

 echo
 cd /d D:\WaitForCompress
 7z a -ttar -so * | 7z a -tgzip -si ..\Compressed\Compressed.tar.gz

.tar.gz文件的生成

双击Run.bat，可以实现将WaitForCompress文件夹中的文件压缩成.tar.gz格式的文件，并自动将压缩文件保存到Compressed文件夹中。

.tar.gz格式文件的验证

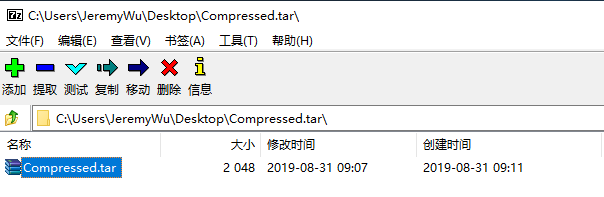
1：打开7-Zip软件，在7-Zip软件中打开Compressed.tar.gz文件；

2：选中Compressed.tar.gz文件，点击提取，选择提取到桌面；

3：在7-Zip软件中打开桌面Compressed.tar文件；

4：选中Compressed.tar文件，点击提取，选择提取到桌面；

最终两次解压后，得到我们最初压缩之前的文件。

Windows系统下，Delphi调用API函数和7z.dll动态库，自动把文件压缩成.tar.gz格式的文件

思路如下：

1：新建txt文件，将如下内容写入进去，保存退出，修改文件后缀为.bat；

2：调用Windows API函数执行.bat文件，即可得到.tar.gz文件。

 echo
 cd /d D:\WaitForCompress
 7z a -ttar -so * | 7z a -tgzip -si ..\Compressed\Compressed.tar.gz

procedure CreateTxtFile(FileName, V_str: string);
var
  F: Textfile; {定义 F 为 Textfile}
begin
  AssignFile(F, FileName); {将文件名与变量 F 关联}
  ReWrite(F); {创建Txt文档并命名为 “FileName ” }
  Writeln(F, V_str);
  Closefile(F); {关闭文件 F}
end;

//执行D:\Run.bat文件
WinExec(PChar('cmd.exe /k d:\run.bat'), SW_HIDE);
//为防止异常等待一会，事件根据实际情况调整，也可以根据文件大小动态生成等待时间
Sleep();

作者：Jeremy.Wu
  出处：https://www.cnblogs.com/jeremywucnblog/

  本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。