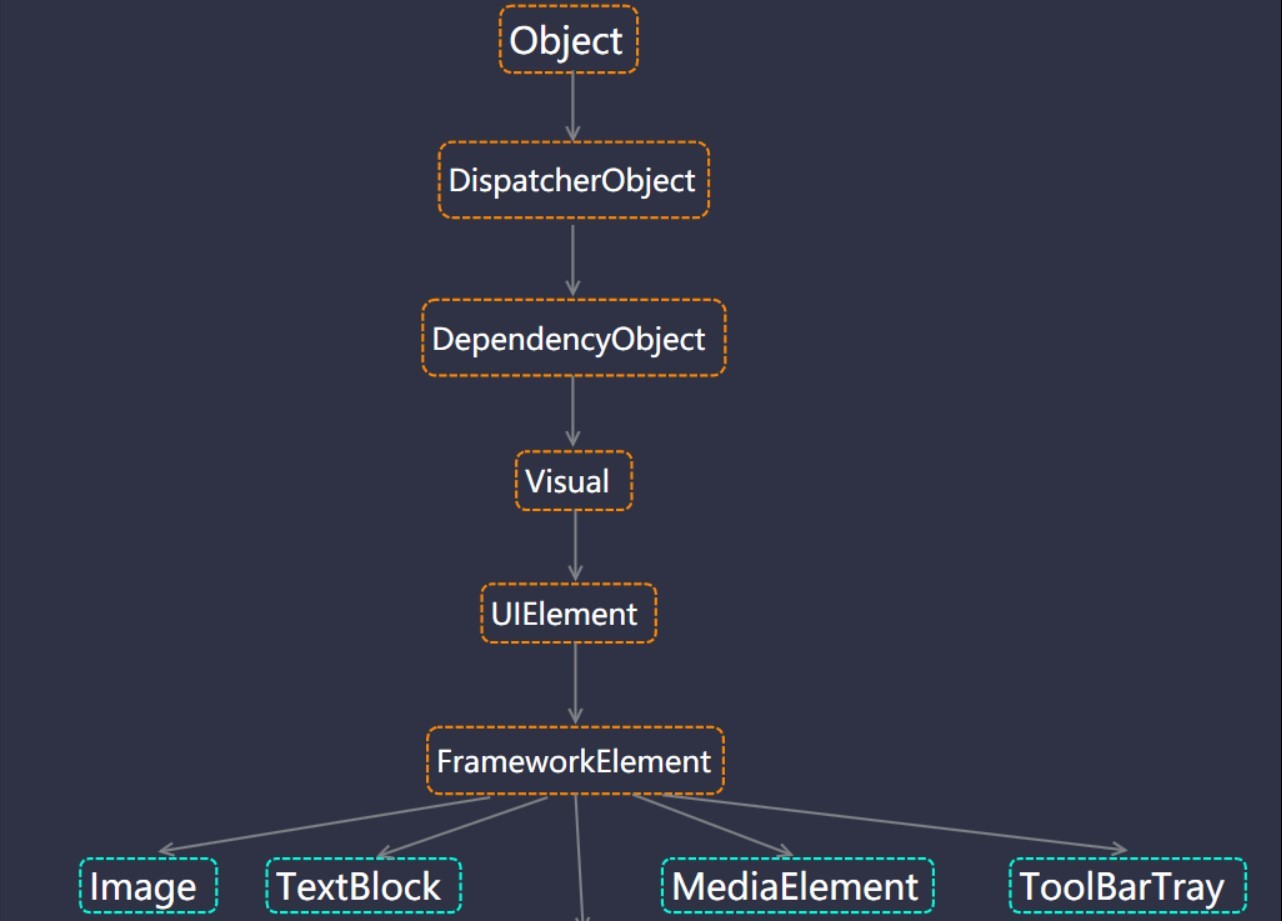
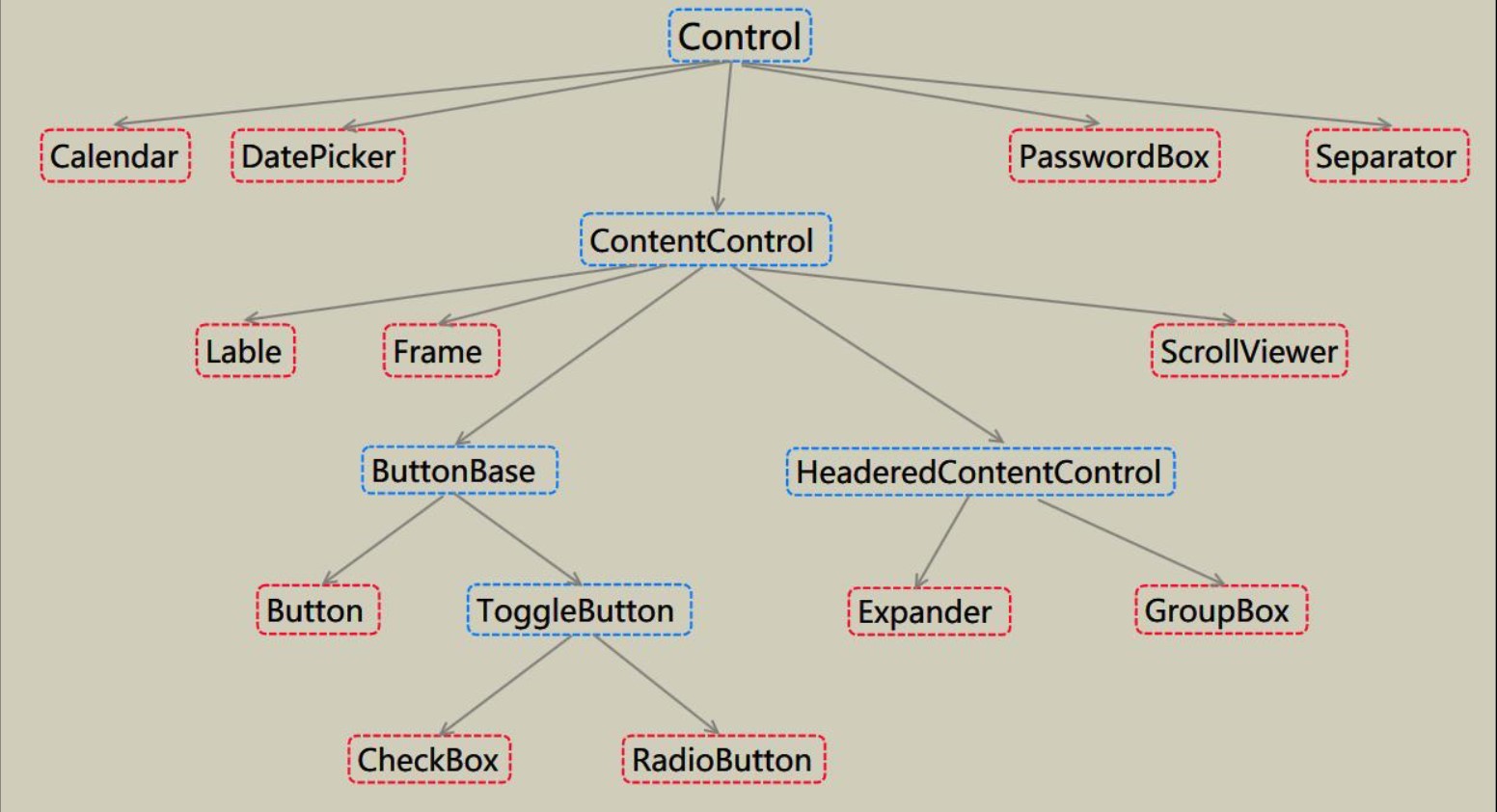
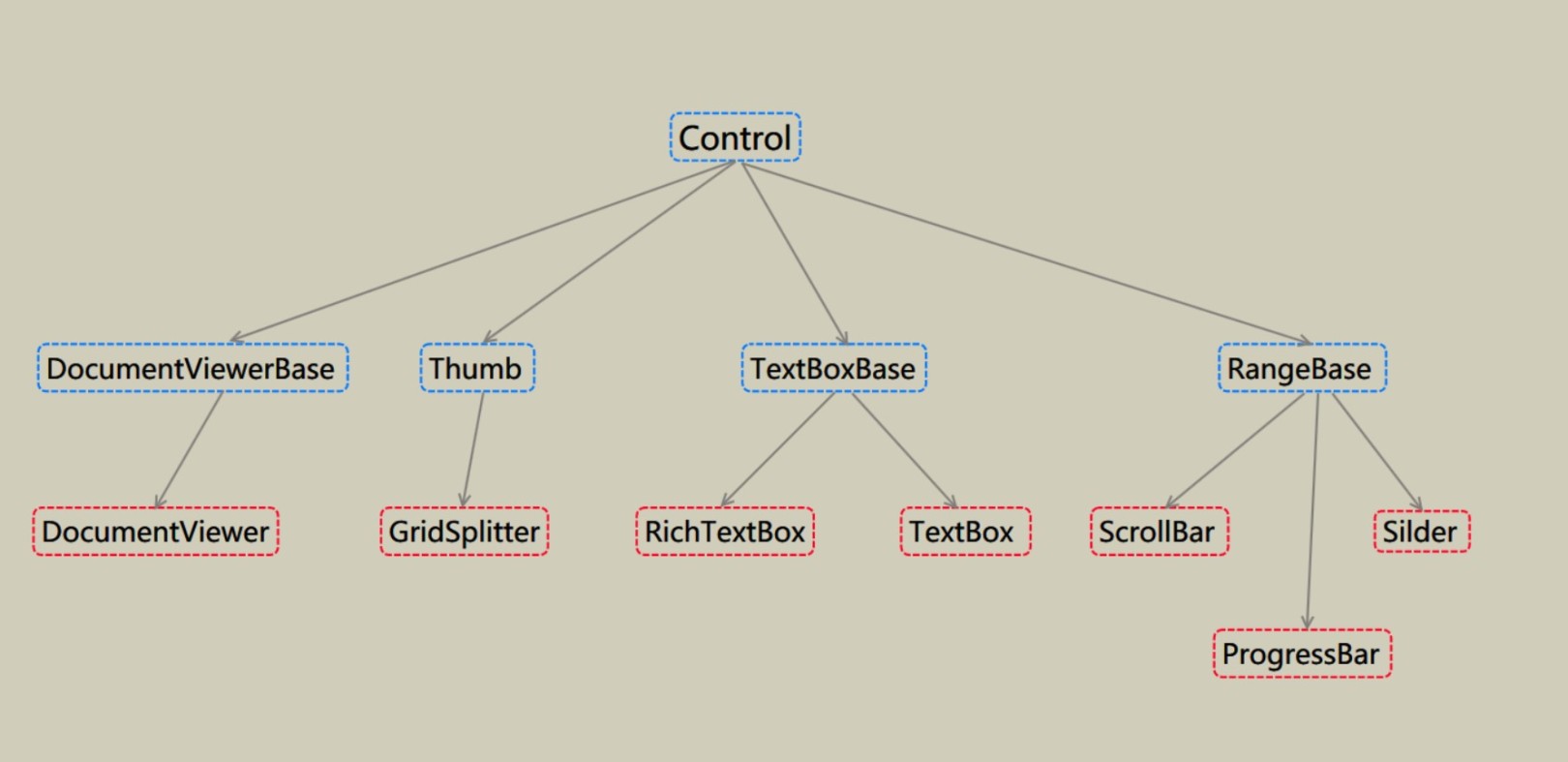
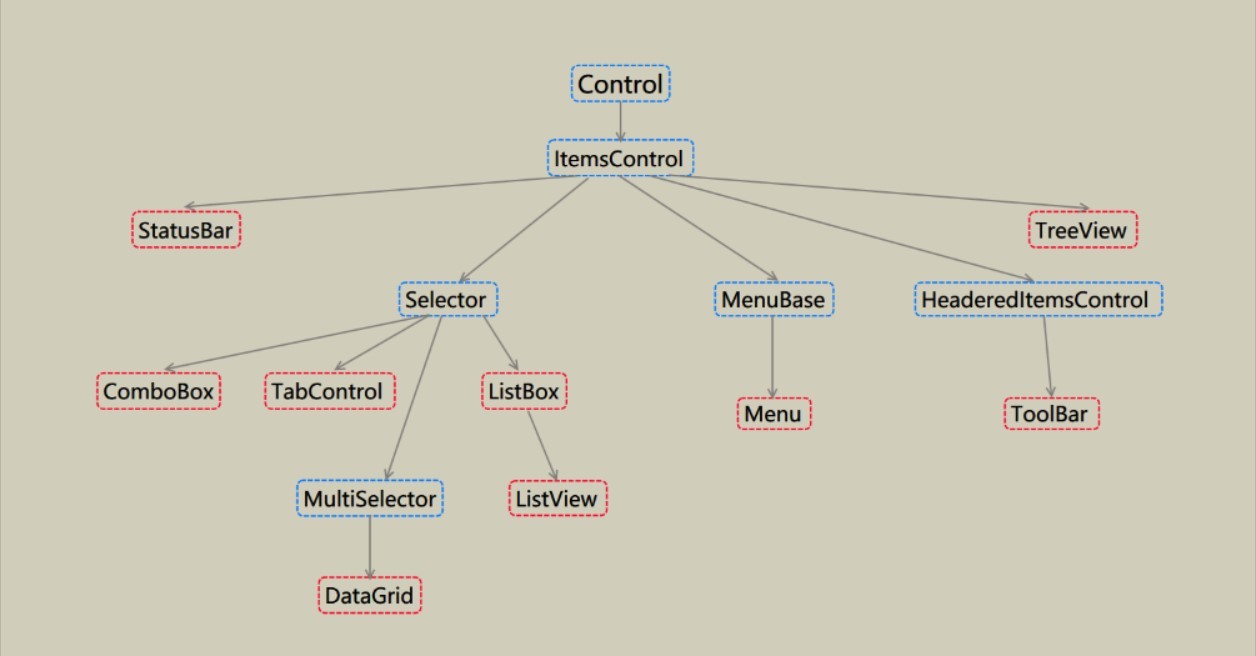
wpf的控件树
转载自:控件树
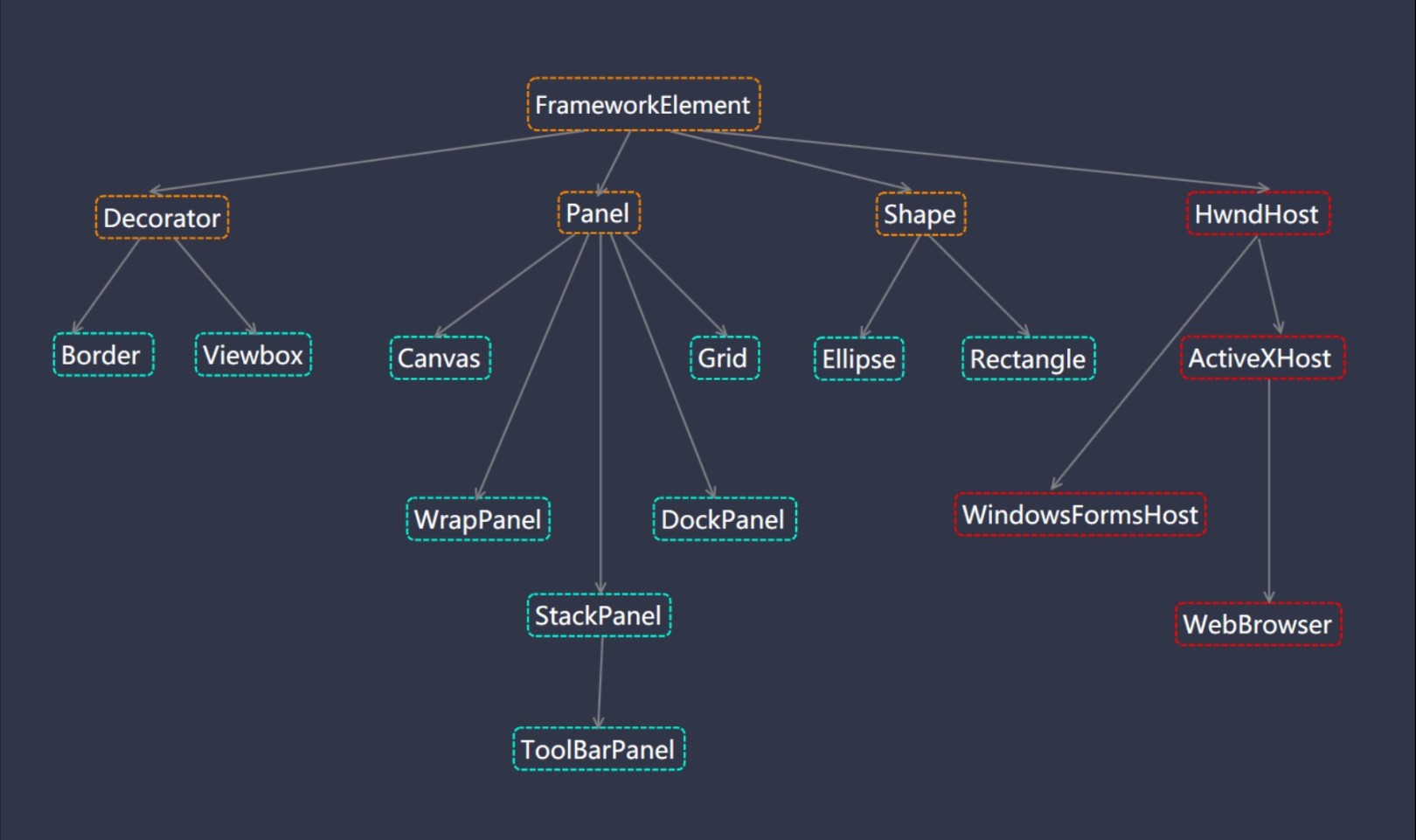
wpf的控件树的更多相关文章
- WPF 控件树
WPF控件树按照基类进行分类,记录下来便于编写自定义控件时查阅 RangeBase范围控件 Thumb拖到控件 TextBoxBase文本控件 ItemControl组控件 ContrentContr ...
- WPF关于控件 父级控件,子级控件,控件模板中的控件,等之间的相互访问
原文:WPF关于控件 父级控件,子级控件,控件模板中的控件,等之间的相互访问 1,在菜单中访问 弹出菜单的控件 var mi = sender as MenuItem;//菜单条目 MenuItem ...
- WPF Popup 控件导致被遮挡内容不刷新的原因
WPF Popup 控件导致被遮挡内容不刷新的原因 周银辉 今天在写一个WPF控件时用到了Popup控件,很郁闷的情况是:当popup关闭时,原来被popup挡住的界面部分不刷新,非要手动刷新一下(比 ...
- 创建 WPF 工具箱控件
创建 WPF 工具箱控件 WPF (Windows Presentation Framework) 工具箱控件模板允许您创建 WPF 控件,会自动添加到 工具箱 安装扩展的安装. 本主题演示如何使用模 ...
- wpf打印控件 实现分页打印控件功能
因为 要实现打印 wpf listbox控件 数据特别多 要打印在 几张纸上 找了几天 都没有找到相关的例子 现在 解决了 在这里和大家分享一下 public void print(Fram ...
- WPF常用控件应用demo
WPF常用控件应用demo 一.Demo 1.Demo截图如下: 2.demo实现过程 总体布局:因放大缩小窗体,控件很根据空间是否足够改变布局,故用WrapPanel布局. <ScrollVi ...
- WPF 分页控件 WPF 多线程 BackgroundWorker
WPF 分页控件 WPF 多线程 BackgroundWorker 大家好,好久没有发表一篇像样的博客了,最近的开发实在头疼,很多东西无从下口,需求没完没了,更要命的是公司的开发从来不走正规流程啊, ...
- WPF Image控件中的ImageSource与Bitmap的互相转换
原文:WPF Image控件中的ImageSource与Bitmap的互相转换 1.从bitmap转换成ImageSource [DllImport("gdi32.dll", ...
- 【转】WPF - 第三方控件
WPF - 第三方控件 目前第三方控件在网上形成巨大的共享资源,其中包括收费的也有免费的,有开源的也有不开源的,合理的使用第三方控件将使项目组的工作事半功倍.比如项目中有些复杂的业务逻辑.有些绚丽的效 ...
随机推荐
- go-数据结构
数据结构 数据结构(算法)的介绍 数据结构的介绍 1) 数据结构是一门研究算法的学科,只从有了编程语言也就有了数据结构.学好数据结构可以编写 出更加漂亮,更加有效率的代码. 2) 要学习好数据结构就要 ...
- CSS @charset规则
定义和用法 @charset规则指定样式表中使用的字符编码.@charset规则必须在样式表中的第一元素,而不是由任何字符之后进行.在外部样式文件中使用.如果@charset定义了多个规则,则仅使用第 ...
- Spring Boot2.1.7启动zipkin-server报错:Error creating bean with name 'armeriaServer' defined in class path
修改项目,更新组件版本时,引入了最新版本2.12.9的zipkin-server和zipkin-autoconfigure-ui时,服务启动报错: org.springframework.beans. ...
- Spring Cloud Gateway报错:Unable to start embedded Tomcat
最近搭建Spring Cloud Gateway时启动项目出现如下报错信息: Error starting ApplicationContext. To display the conditions ...
- Python—路由追踪(并生成追踪图片)
需要先安装两个包 [root@localhost ~]# yum install graphviz // 为了使用dot命令 [root@localhost ~]# yum install Image ...
- JAVA学习方法之——费曼学习法
理查德·费曼 费曼简介 理查德·菲利普斯·费曼(Richard Phillips Feynman),出生于1918年5月11日,是美籍犹太裔物理学家,曾在1965年获得诺贝尔物理学奖,也被认为是继爱因 ...
- vue全局路由守卫beforeEach+token验证+node
在后端安装jsonwebtoken npm i jsonwebtoken --save 在 login.js文件中引入 // 引入jwtconst jwt = require ...
- Node.js—学习
一.Node.js 1. Hello World var http = require('http'); http.createServer(function(request, response) { ...
- unittest,requests,assertEqual实战演练
请求方式:POST请求url:https://api.apiopen.top/developerLogin请求参数:名称 类型 必须 描述 示例name string 是 账号 peakchaopas ...
- LeetCode 二进制问题
338. Counting Bits(计算小于n的各个数值对应的二进制1的个数) 思路:通过奇偶判断,if i是偶数,a[i]=a[i/2],if i是奇数,a[i]=a[i-1]+1. class ...
