从2-3-4树到红黑树(下) Java与C的实现
欢迎探讨，如有错误敬请指正
如需转载，请注明出处 http://www.cnblogs.com/nullzx/
相关博客：
1. 实现技巧
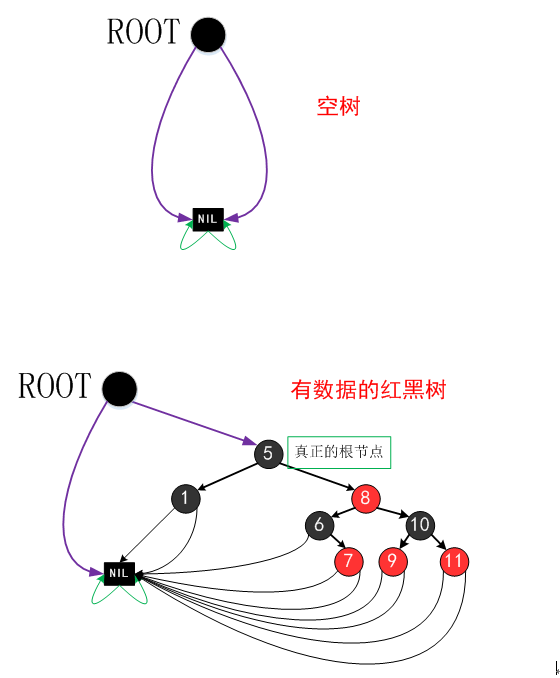
为了简化代码和减少不必要的开销，在具体的实现中我们定义一个伪根节点ROOT且只定义一个NIL节点。伪根节点的左子支永远指向NIL节点，NIL节点的左右子支又指向它自身。伪根节点的右子支才表示真正的红黑树。
2. Java语言实现
package datastruct;
import java.util.Comparator;
public class RBtree<E> {
private static class Node<E>{
E e;
boolean color;
Node<E> left;
Node<E> right;
Node<E> parent;
public Node(E e, boolean color, Node<E> left, Node<E> right, Node<E> parent){
this.e = e;
this.color = color;
this.left = left;
this.right = right;
this.parent = parent;
}
public boolean isRead(){
return color;
}
}
public static final boolean RED = true;
public static final boolean BLACK = false;
//所有叶子节点的左右子支都指向同一个NIL节点,NIL节点的父节点指向null
private final Node<E> NIL;
private final Node<E> ROOT;//指向伪根节点的引用
private int size = 0;//节点个数
Comparator<? super E> cmp;//节点大小的比较器
//如果调用了不带参数的构造函数，则使用该内部类作为比较器，
//但此时泛型E需要继承Comparable接口,否则运行时会抛出异常
private static class Cmp<T> implements Comparator<T>{
@SuppressWarnings({ "unchecked", "rawtypes" })
@Override
public int compare(T e1, T e2) {
return ((Comparable)e1).compareTo(e2);
}
}
//不带比较器的构造函数
public RBtree(){
ROOT = new Node<E>(null, BLACK, null, null, null);
NIL = new Node<E>(null, BLACK, null, null, null);
NIL.left = NIL;
NIL.right = NIL;
ROOT.left = NIL;
ROOT.right = NIL;
ROOT.parent = ROOT;
cmp = new Cmp<E>();
}
//带比较器的构造函数
public RBtree(Cmp<? super E> cmp){
if(cmp == null){
throw new IllegalArgumentException();
}
this.cmp = cmp;
//创建一个伪根节点，该节点的右子支才是真正的RBtree树的根,同时该节点还作为NIL节点
//使用伪根节点节点的目的是，对插入和删除操作递归的形式能够统一
ROOT = new Node<E>(null, BLACK, null, null, null);
NIL = new Node<E>(null, BLACK, null, null, null);
NIL.left = NIL;
NIL.right = NIL;
ROOT.left = NIL;
ROOT.right = NIL;
ROOT.parent = ROOT;
}
//逆时针旋转（左旋），参数表示轴节点
private void antiClockwiseRotate(Node<E> X){
Node<E> P = X.parent;
Node<E> XR = X.right;
if(P.left == X){
P.left = XR;
}else{
P.right = XR;
}
XR.parent = P;
X.right = XR.left;
if(XR.left != NIL){
XR.left.parent = X;
}
XR.left = X;
X.parent = XR;
}
//顺时针旋转（右旋）,参数表示轴节点
private void clockwiseRotate(Node<E> X){
Node<E> P = X.parent;
Node<E> XL = X.left;
if(P.left == X){
P.left = XL;
}else{
P.right = XL;
}
XL.parent = P;
X.left = XL.right;
if(XL.right != NIL){
XL.right.parent = X;
}
XL.right = X;
X.parent = XL;
}
private Node<E> min(Node<E> X){
while(X.left != NIL){
X = X.left;
}
return X;
}
public int size(){
return size;
}
public boolean contain(E e){
Node<E> X = ROOT.right;
while(X != NIL){
int r = cmp.compare(e, X.e);
if(r > 0){
X = X.right;
}else
if(r < 0){
X = X.left;
}else{
return true;
}
}
return false;
}
public boolean insert(E e){
Node<E> P = ROOT;
Node<E> X = ROOT.right;
int r = 0;
while(X != NIL){
r = cmp.compare(e, X.e);
P = X;
if(r > 0){
X = X.right;
}else
if(r < 0){
X = X.left;
}else{
return false;//元素已存在，插入失败
}
}
Node<E> G;
Node<E> U;
X = new Node<E>(e, RED, NIL, NIL, P);//插入的新节点涂红
if(r >= 0){//考虑到首次插入的情况，这个等号是必须的
P.right = X;
}else{
P.left = X;
}
while(true){
P = X.parent;
//红父
if(P.isRead()){
G = P.parent;
if(P == G.left){
U = G.right;
}else{
U = G.left;
}
//红叔
if(U.isRead()){
P.color = BLACK;
U.color = BLACK;
G.color = RED;
X = G;//继续向上回溯
}else{//黑叔
if(G.left == P){
if(P.left == X){
clockwiseRotate(G);
P.color = BLACK;
G.color = RED;
}else{
antiClockwiseRotate(P);
clockwiseRotate(G);
X.color = BLACK;
G.color = RED;
}
}else{
if(P.right == X){
antiClockwiseRotate(G);
P.color = BLACK;
G.color = RED;
}else{
clockwiseRotate(P);
antiClockwiseRotate(G);
X.color = BLACK;
G.color = RED;
}
}
break;
}
}else{//黑父
break;
}
}
size++;
ROOT.right.color = BLACK;//有可能向上层进位，根节点图黑
return true;
}
public boolean delete(E e){
Node<E> X = ROOT.right;
X.color = RED; //删除时，根先涂红，1.防止继续向上回溯 2.只有根节点时也方便删除
Node<E> P;
Node<E> B;
while(X != NIL){
int r = cmp.compare(e, X.e);
if(r > 0){
X = X.right;
}else
if(r < 0){
X = X.left;
}else{
break;
}
}
if(X == NIL){//没有找到需要删除的节点
ROOT.right.color = BLACK;
return false;
}
size--;//一定可以删除一个节点
if(X.left != NIL && X.right != NIL){
Node<E> tmp = min(X.right);
X.e = tmp.e;
X = tmp;
}
P = X.parent;
if(X.right != NIL){
if(X == P.left){
P.left = X.right;
}else{
P.right = X.right;
}
X.right.parent = P;
X.color = BLACK;
ROOT.right.color = BLACK;
return true;
}else
if(X.left != NIL){
if(X == P.left){
P.left = X.left;
}else{
P.right = X.left;
}
X.left.parent = P;
X.color = BLACK;
ROOT.right.color = BLACK;
return true;
}else{
if(X == P.left){
P.left = NIL;
}else{
P.right = NIL;
}
if(X.isRead()){
ROOT.right.color = BLACK;
return true;
}else{
X = NIL;
}
}
//要删除的是叶子节点
//四中情况调整
while(true){
if(X == P.left){
B = P.right;
}else{
B = P.left;
}
if(!B.isRead()){//黑兄
Node<E> BL = B.left;//左侄子
Node<E> BR = B.right;//右侄子
if(B.left.isRead() || B.right.isRead()){//红侄
if(X == P.left){
if(BR.isRead()){
antiClockwiseRotate(P);
BR.color = BLACK;
B.color = P.color;
P.color = BLACK;
}else{
clockwiseRotate(B);
antiClockwiseRotate(P);
BL.color = P.color;
P.color = BLACK;
}
}else{
if(BL.isRead()){
clockwiseRotate(P);
BL.color = BLACK;
B.color = P.color;
P.color = BLACK;
}else{
antiClockwiseRotate(B);
clockwiseRotate(P);
BR.color = P.color;
P.color = BLACK;
}
}
break;//不需要继续向上回溯
}else{
if(P.isRead()){//黑侄红父
P.color = BLACK;
B.color = RED;
break;//不需要继续向上回溯
}else{//黑侄黑父,继续向上回溯
B.color = RED;
X = P;
P = X.parent;
}
}
}else{//红兄，变换一下红黑树的形状，继续判断
if(B == P.right){
antiClockwiseRotate(P);
}else{
clockwiseRotate(P);
}
B.color = BLACK;
P.color = RED;
//X节点的P节点没有发生变化，但兄弟节点发生变化
}
}
ROOT.right.color = BLACK;
return true;
}
public void preorderTraverse(){
preorderTraverse0(ROOT.right);
}
private void preorderTraverse0(Node<E> X){
if(X != NIL){
System.out.print(X.e + " " + (X.isRead() ? "RED " : "BLACK") + " :");
if(X.left != NIL){
System.out.print(X.left.e + " ");
}else{
System.out.print("NIL ");
}
if(X.right != NIL){
System.out.print(X.right.e + " ");
}else{
System.out.print("NIL ");
}
System.out.println();
preorderTraverse0(X.left);
preorderTraverse0(X.right);
}
}
public static void main(String[] args){
RBtree<Integer> rbt = new RBtree<Integer>();
rbt.insert(50);
rbt.insert(25);
rbt.insert(75);
rbt.insert(10);
rbt.insert(30);
rbt.insert(27);
rbt.insert(35);
rbt.insert(40);
rbt.insert(31);
rbt.insert(55);
rbt.insert(80);
rbt.insert(90);
// rbt.insert(22);
// rbt.insert(5);
// rbt.delete(5);
// rbt.delete(51);
// rbt.delete(80);
// rbt.delete(50);
// rbt.delete(75);
// rbt.delete(27);
// rbt.delete(10);
// rbt.delete(25);
rbt.delete(10);
rbt.preorderTraverse();
System.out.println();
System.out.println("size: " + rbt.size());
System.out.println(rbt.contain(40));
}
}
3. C语言实现
下面的C语言实现是自顶向下的方式实现的，即采用了预合并和预分裂的方法，详情请见本博客 从2-3-4到红黑树（上）。在此方法中我们将伪根节点的数据定义为负无穷，这样插入和删除操作可以直接从伪根节点开始。
"RBtree.h"中的文件内容
#ifndef __RBTREE_H__
#define __RBTREE_H__ typedef enum{Red,Black} colorType;
typedef struct Node{
int data;
struct Node* left;
struct Node* right;
colorType color;
}Node,*RBtree; int Insert(RBtree* T, int argD);
int Delete(RBtree* T, int argD);
int Find(RBtree T,int argD);
int InOredrTraverse(RBtree T);
int PreOredrTraverse(RBtree T);
int Destroy(RBtree* T); #endif
RBtree.c中的内容
#include "RBtree.h"
#include <limits.h>
#include <stdlib.h>
#include <stdio.h> static int Init(RBtree* T);
static int FindMin(Node* ptr,RBtree NullNode);
static void RightRotate(RBtree* T);
static void LeftRotate(RBtree* T); static void RightPreOrderTra(RBtree ptr,RBtree NullNode);
static void RightInOrderTra(RBtree ptr,RBtree NullNode);
static void RightPostOrderTra(RBtree ptr,RBtree NullNode); int Insert(RBtree* T, int argD){
Node *X,*P,*GP,*GGP,*NullNode;
Node **tmp;
if(T == NULL){
return -1;
} if(*T == NULL){
if(Init(T) == -1){
return -1;
}
} GP = NULL;
GGP = NULL;
P = NULL;
X = (*T);//从头结点开始，防止插入负无穷
NullNode = (*T)->left;
NullNode->data = argD; while(X->data != argD){
if(X->left->color == Red && X->right->color == Red){
X->color = Red;
X->left->color = Black;
X->right->color = Black; if(P->color == Red){
if(argD > GGP->data){
tmp = &(GGP->right);
}else{
tmp = &(GGP->left);
} if(argD > GP->data){
if(argD > P->data){
LeftRotate(tmp);
P->color = Black;
GP->color = Red;
GP = GGP; //为能够正确下落一层做保证
}else{
RightRotate(&(GP->right));
LeftRotate(tmp);
X->color = Black;
GP->color = Red;
P = X;//为能够正确下落一层做保证
GP = P;//为能够正确下落一层做保证
}
}else{
if(argD < P->data){
RightRotate(tmp);
P->color = Black;
GP->color = Red;
GP = GGP;
}else{
LeftRotate(&(GP->left));
RightRotate(tmp);
X->color = Black;
GP->color = Red;
P = X;
GP = P;
}
}
}
} GGP = GP; GP = P; P = X;
if(argD > X->data){
X = X->right;
}
else{
X = X->left;
} } if(X != NullNode){
(*T)->right->color = Black;
return -1;
} X = (Node*)malloc(sizeof(Node));
if(X == NULL){
(*T)->right->color = Black;
return -1;
} X->color = Red;
X->data = argD;
X->left = X->right = NullNode;
if(argD > P->data){
P->right = X;
}
else{
P->left = X;
} if(P->color == Red){
if(argD > GGP->data){
tmp = &(GGP->right);
}else{
tmp = &(GGP->left);
} if(argD > GP->data){
if(argD > P->data){
LeftRotate(tmp);
P->color = Black;
GP->color = Red;
GP = GGP;
}else{
RightRotate(&(GP->right));
LeftRotate(tmp);
X->color = Black;
GP->color = Red;
P = X;
GP = P;
}
}else{
if(argD < P->data){
RightRotate(tmp);
P->color = Black;
GP->color = Red;
GP = GGP;
}else{
LeftRotate(&(GP->left));
RightRotate(tmp);
X->color = Black;
GP->color = Red;
P = X;
GP = P;
}
}
} (*T)->right->color = Black;
return 0;
} int Delete(RBtree* T,int argD){
Node *X,*B,*P,*GP,*NullNode;
RBtree *tmp;
if(T == NULL || *T == NULL){
return -1;
} P = *T;
X = (*T)->right;//X从root开始，防止删除负无穷
NullNode = (*T)->left;
B = NullNode;
GP = NULL;
(*T)->right->color = Red;//根涂红 while(1){
if(X == NullNode){
(*T)->right->color = Black;
return -1;//删除元素不存在
} if(X->color == Black){
if(X->left->color == Black && X->right->color == Black){
if(B->color == Red){
if(GP->right == P){
tmp = &(GP->right);
}else{
tmp = &(GP->left);
} B->color = Black;
P->color = Red;
if(P->right == X){
RightRotate(tmp);
B = P->left;
GP = *tmp;
}else{
LeftRotate(tmp);
B = P->right;
GP = *tmp;
}
} if(B->color == Black){
if(B->left->color == Black && B->right->color == Black){
P->color = Black;
X->color = Red;
B->color = Red;
}else{
if(GP->right == P){
tmp = &(GP->right);
}else{
tmp = &(GP->left);
} if(P->right == X){
if(B->left->color == Red){
P->color = Black;
X->color = Red;
B->color = Red;
B->left->color = Black;
RightRotate(tmp);
}else
if(B->right->color == Red){
P->color = Black;
X->color = Red;
LeftRotate(&(P->left));
RightRotate(tmp);
}
}else{
if(B->right->color == Red){
P->color = Black;
X->color = Red;
B->color = Red;
B->right->color = Black;
LeftRotate(tmp);
}else
if(B->left->color == Red){
P->color = Black;
X->color = Red;
RightRotate(&(P->right));
LeftRotate(tmp);
}
}
}
}
}
} if(X->data == argD){
if(X->left != NullNode && X->right != NullNode){
argD = FindMin(X->right,(*T)->left);
X->data = argD;
GP = P;
P = X;
X = P->right;
B = P->left;
}else
if(X->left == NullNode && X->right == NullNode){
if(P->right == X){
P->right = NullNode;
}
else{
P->left = NullNode;
}
free(X); if((*T)->left == NullNode && (*T)->right == NullNode){
free(NullNode);
free(*T);
*T = NULL;
return 0;
}
(*T)->right->color = Black;
return 0;
}else
if(X->left != NullNode){
X->data = X->left->data;
free(X->left);
X->left = NullNode;
(*T)->right->color = Black;
return 0;
}else
if(X->right != NullNode){
X->data = X->right->data;
free(X->right);
X->right = NullNode;
(*T)->right->color = Black;
return 0;
}
}else
if(argD > X->data){
GP = P;
P = X;
X = P->right;
B = P->left;
}else
if(argD < X->data){
GP = P;
P = X;
X = P->left;
B = P->right;
}
}
} int Find(RBtree T,int argD){
if(T != NULL){
Node* root = T->right;
Node* NullNode = T->left;
while(root != NullNode){
if(root->data == argD){
return 0;
}else
if(argD > root->data){
root = root->right;
}else{
root = root->left;
}
}
}
return -1; } int InOredrTraverse(RBtree T){
if(T == NULL){
return -1;
}
RightInOrderTra(T->right, T->left);
return 0;
} int PreOredrTraverse(RBtree T){
if(T == NULL){
return -1;
}
RightPreOrderTra(T->right,T->left);
return 0;
} int Destroy(RBtree* T){
if(*T == NULL){
return -1;
}
RightPostOrderTra((*T)->right, (*T)->left);
free((*T)->left);
free((*T));
*T = NULL;
return 0;
} static void RightInOrderTra(RBtree ptr,RBtree NullNode){
if(ptr != NullNode){
RightInOrderTra(ptr->left,NullNode);
printf("% 3d",ptr->data);
RightInOrderTra(ptr->right,NullNode);
}
} static void RightPreOrderTra(RBtree ptr,RBtree NullNode){
if(ptr != NullNode){
printf("%3d:%c(%3d,%3d)\n",
ptr->data,ptr->color == Red? 'R':'B',
ptr->left == NullNode?-1:ptr->left->data,
ptr->right == NullNode?-1 :ptr->right->data
);
RightPreOrderTra(ptr->left,NullNode);
RightPreOrderTra(ptr->right,NullNode);
}
} static void RightPostOrderTra(RBtree ptr,RBtree NullNode){
if(ptr != NullNode){
RightPostOrderTra(ptr->left,NullNode);
RightPostOrderTra(ptr->right,NullNode);
free(ptr);
}
} static int Init(RBtree* T){
Node* tmp;
tmp = (Node*)malloc(sizeof(Node));
*T = (Node*)malloc(sizeof(Node));
if(*T == NULL || tmp == NULL){
return -1;
}
(*T)->data = INT_MIN;
(*T)->color = Black;
(*T)->left = (*T)->right = tmp;
tmp->color = Black;
tmp->left = tmp->right = tmp;
return 0;
} static void RightRotate(RBtree* T){
Node* Parent = (*T);
Node* LeftSon = (*T)->left;
Parent->left = LeftSon->right;
LeftSon->right = Parent;
*T = LeftSon;
} static void LeftRotate(RBtree* T){
Node* Parent = (*T);
Node* RightSon = (*T)->right;
Parent->right = RightSon->left;
RightSon->left = Parent;
*T = RightSon;
}
static int FindMin(Node* ptr,RBtree NullNode){
while(ptr->left != NullNode){
ptr = ptr->left;
}
return ptr->data;
}
从2-3-4树到红黑树(下) Java与C的实现的更多相关文章
- 论AVL树与红黑树
首先讲解一下AVL树: 例如,我们要输入这样一串数字,10,9,8,7,15,20这样一串数字来建立AVL树 1,首先输入10,得到一个根结点10 2,然后输入9, 得到10这个根结点一个左孩子结点9 ...
- 浅谈算法和数据结构: 七 二叉查找树 八 平衡查找树之2-3树 九 平衡查找树之红黑树 十 平衡查找树之B树
http://www.cnblogs.com/yangecnu/p/Introduce-Binary-Search-Tree.html 前文介绍了符号表的两种实现,无序链表和有序数组,无序链表在插入的 ...
- 二叉排序树、平衡二叉树、B树&B+树、红黑树的设计动机、缺陷与应用场景
之前面试时曾被问到"如果实现操作系统的线程调度应该采用什么数据结构?",因为我看过ucore的源码,知道ucore是采用斜堆的方式实现的,可以做到O(n)的插入.O(1)的查找.我 ...
- 单例模式，堆，BST，AVL树，红黑树
单例模式 第一种(懒汉,线程不安全): public class Singleton { private static Singleton instance; private Singleton () ...
- 二叉树，AVL树和红黑树
为了接下来能更好的学习TreeMap和TreeSet,讲解一下二叉树,AVL树和红黑树. 1. 二叉查找树 2. AVL树 2.1. 树旋转 2.1.1. 左旋和右旋 2.1.2. 左左,右右,左右, ...
- B树，B+树，红黑树应用场景AVL树，红黑树，B树，B+树，Trie树
B B+运用在file system database这类持续存储结构,同样能保持lon(n)的插入与查询,也需要额外的平衡调节.像mysql的数据库定义是可以指定B+ 索引还是hash索引. C++ ...
- [BinaryTree] AVL树、红黑树、B/B+树和Trie树的比较
转自:AVL树.红黑树.B/B+树和Trie树的比较 AVL树 最早的平衡二叉树之一.AVL是一种高度平衡的二叉树,所以通常的结果是,维护这种高度平衡所付出的代价比从中获得的效率收益还大,故而实际的应 ...
- AVL树与红黑树
平衡树是平时经常使用数据结构. C++/JAVA中的set与map都是通过红黑树实现的. 通过了解平衡树的实现原理,可以更清楚的理解map和set的使用场景. 下面介绍AVL树和红黑树. 1. AVL ...
- AVL树，红黑树，B-B+树，Trie树原理和应用
前言:本文章来源于我在知乎上回答的一个问题 AVL树,红黑树,B树,B+树,Trie树都分别应用在哪些现实场景中? 看完后您可能会了解到这些数据结构大致的原理及为什么用在这些场景,文章并不涉及具体操作 ...
随机推荐
- 爬虫研究-主要针对ali
公司一个同事想爬取ali的网页受挫,自己跟着尝试了下,发现存在anti-spdier.准备了解下反爬虫,看怎么处理ali. http://www.freebuf.com/news/topnews/96 ...
- Spring AOP详解
一.前言 在以前的项目中,很少去关注spring aop的具体实现与理论,只是简单了解了一下什么是aop具体怎么用,看到了一篇博文写得还不错,就转载来学习一下,博文地址:http://www.cnbl ...
- compass typography 排版 常用排版方法[Sass和compass学习笔记]
Bullets 用来定义ul li 相关的样式 no-bullet 关闭 li的默认样式 那个小圆点 no-bullets 作用域ul 调用no-bullet 函数 不过用了reset 后 默认没有 ...
- vmware下的centos上网配置
设置网络 1.查看网络配制 刚刚安装好的虚拟机,里面还是原始的网络配制.只有一个回环网卡. 通过ifconifg命令可以查看到. 2.添加网卡 从上面看到只有回环网卡,现在需要添加一块网卡来进行后 ...
- 匿名对象 构造方法 重载 构造代码块 this 关键字
一.匿名对象 1.匿名对象 :没有名字对象 2.匿名对象的使用注意点: 1.我们一般不会用匿名对象给属性赋值,无法获取属性值. 2.匿名对象永远都不可能事一个对象. 3.匿名对象的好处 : 书写简单. ...
- RDLC报表数据工具栏关闭后打开方法
显示方法为:Ctrl + Alt + D 快捷键 只做自己记录用
- 设计模式（十二）：bridge模式
刚开始看到这个模式并不是很理解,之后在网上看到别人的博客,才大致抓住了脉络. 何谓抽象和实现分离:就是将一个实际的物件跟它的所具有的功能分离.<大话设计模式>中有对手机品牌和具体的手机应用 ...
- git使用手册
1.git常用命令 >>首先做git clone 形成本地repository: >>然后做checkout形成分支 列出所有分支 $ git branch –r 切换到新分 ...
- Unity之CharacterController 碰撞问题总结
CharacterController 不会受到scene的重力影响,自带物理碰撞检测,在脱离导航网格的应用场景下(比如飞行),是很有优势的Unity原生工具组件.如果在复杂的应用场景里,会有多种CC ...
- Django发送邮件
1. 配置相关参数 如果用的是 阿里云的企业邮箱,则类似于下面: 在 settings.py 的最后面加上这些 EMAIL_BACKEND='django.core.mail.backends.smt ...