最小生成树算法Kruskal详解

要讲Kruskal，我们先来看下面一组样例。

4 5
1 2 3
1 4 5
2 4 7
2 3 6
3 4 8

14

　　

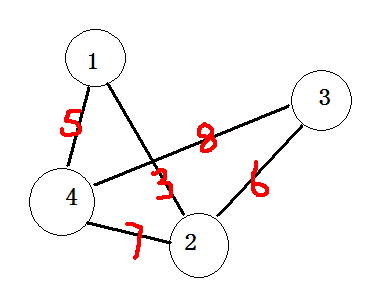
画出来更直观一些，就是上面的这张图。

智商只要不是0的（了解最小生成树是什么的童鞋）应该都知道要选择1<->4, 1<->2, 2<->3这三条边那么大家就会问为什么选择这三条呢。

一棵树边的数量等于这棵输的点的数量减1。（不信自己画画试试）这里不再解释。

假设有N个点，那么我们肯定要选择n-1条边来生成一棵树。这棵树就是这张图的生成树。

很显然生成树有一堆。

而最小生成树是指边权之和最小的生成树。那么我们自然而然的想到了贪心!!!

没错，就是贪心，我们按照边的权值进行贪心。

同时为了保证到最后所有的点都连在了一起，并且没有多余的边。我们就要用到并查集。只要两个顶点被一条边所连接。那么他们就有一个共同的祖先。我们在以后就只要判断一下，只要两个顶点没有共同祖先，就可以将他们连入生成树中。当边的条数加到n-1时，我们就可以结束了。

下面是代码

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

int n, m;
int f[];
int sum, tot;
struct edge{
    int u, v, w;
}ed[];

bool cmp(edge a, edge b) {
    return a.w < b.w;
}

int find(int x) {
    if(x == f[x]) return x;
    else return f[x] = find(f[x]);
}

int main() {
    scanf("%d%d", &n, &m);
    for(int i=; i<=n; i++) {
        f[i] = i;
    }
    for(int i=; i<=m; i++) {
        scanf("%d%d%d", &ed[i].u, &ed[i].v, &ed[i].w);
    }
    sort(ed+, ed++m, cmp);
    for(int i=; i<=m; i++) {
        int xx = find(ed[i].u), yy = find(ed[i].v);
        if(xx != yy) {
            f[xx] = find(yy);
            tot++;
            sum += ed[i].w;
        }
        if(tot == n-) {
            break;
        }
    }
    printf("%d", sum);
}

作者：wlz

出处：http://www.cnblogs.com/bljfy/p/8728133.html

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。